题目内容
（2012•青岛）如图，某校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2米的影子CE；而当光线与地面夹角是45°
时，教学楼顶A在地面上的影子F与墙角C有13米的距离（B、F、C在一条直线上）
（1）求教学楼AB的高度；
（2）学校要在A、E之间挂一些彩旗，请你求出A、E之间的距离（结果保留整数）．
（参考数据：sin22°≈
，cos22°≈
，tan22°≈
）
时，教学楼顶A在地面上的影子F与墙角C有13米的距离（B、F、C在一条直线上）（1）求教学楼AB的高度；
（2）学校要在A、E之间挂一些彩旗，请你求出A、E之间的距离（结果保留整数）．
（参考数据：sin22°≈
| 3 |
| 8 |
| 15 |
| 16 |
| 2 |
| 5 |
分析：（1）首先构造直角三角形△AEM，利用tan22°=
，求出即可；
（2）利用Rt△AME中，cos22°=
，求出AE即可．
| AM |
| ME |
（2）利用Rt△AME中，cos22°=
| ME |
| AE |
解答：
解：（1）过点E作EM⊥AB，垂足为M．
设AB为x．
Rt△ABF中，∠AFB=45°，
∴BF=AB=x，
∴BC=BF+FC=x+13，
在Rt△AEM中，∠AEM=22°，AM=AB-BM=AB-CE=x-2，
tan22°=
，
则
=
，
解得：x=12．
即教学楼的高12m．
（2）由（1）可得ME=BC=x+13=12+13=25．
在Rt△AME中，cos22°=
．
∴AE=
≈
≈27，
即A、E之间的距离约为27m．
解：（1）过点E作EM⊥AB，垂足为M．设AB为x．
Rt△ABF中，∠AFB=45°，
∴BF=AB=x，
∴BC=BF+FC=x+13，
在Rt△AEM中，∠AEM=22°，AM=AB-BM=AB-CE=x-2，
tan22°=
| AM |
| ME |
则
| x-2 |
| x+13 |
| 2 |
| 5 |
解得：x=12．
即教学楼的高12m．
（2）由（1）可得ME=BC=x+13=12+13=25．
在Rt△AME中，cos22°=
| ME |
| AE |
∴AE=
| ME |
| cos22° |
| 25 | ||
|
即A、E之间的距离约为27m．
点评：此题主要考查了解直角三角形的应用，根据已知得出tan22°=
是解题关键．
| AM |
| ME |
练习册系列答案
相关题目
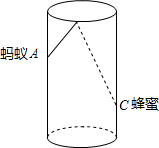（2012•青岛）如图，圆柱形玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底3cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为
（2012•青岛）如图，正方体表面上画有一圈黑色线条，则它的左视图是（ ）
（2012•青岛）如图，在一块长为22米、宽为17米的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分种上草坪，使草坪面积为300平方米．若设道路宽为x米，则根据题意可列出方程为
（2012•青岛）如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，将△ABC绕点C逆时针旋转至△A′B′C′，使得点A′恰好落在AB上，连接BB′，则BB′的长度为