题目内容
 已知,如图△ABC中,AM是BC边上的中线,求证:AM<
已知,如图△ABC中,AM是BC边上的中线,求证:AM<| 1 | 2 |
分析:可延长AM到D,使MD=AM,连CD,则△ABM≌△DCM得AB=CD,进而在△ACD中利用三角形三边关系,证之.
解答: 证明:延长AM到D,使MD=AM,连CD,
证明:延长AM到D,使MD=AM,连CD,
∵AM是BC边上的中线,∴BM=CM,
又AM=DM,∠AMB=∠CMD,
∴△ABM≌△DCM,∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
AM<
(AB+AC).
 证明:延长AM到D,使MD=AM,连CD,
证明:延长AM到D,使MD=AM,连CD,∵AM是BC边上的中线,∴BM=CM,
又AM=DM,∠AMB=∠CMD,
∴△ABM≌△DCM,∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
AM<
| 1 |
| 2 |
点评:本题主要考查了全等三角形的判定及性质以及三角形的三边关系问题,应熟练掌握.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
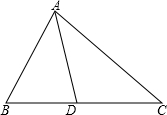 已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD.
已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD. (1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G.
(1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G. 已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE.
已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE. 已知,如图△ABC中,AB=AC,CD⊥AD于D,CD=
已知,如图△ABC中,AB=AC,CD⊥AD于D,CD= 已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为
已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为