Question

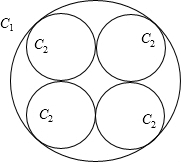
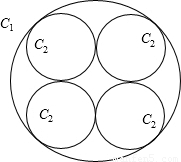
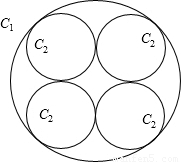
设C₁，C₂，C₃，…为一群圆，其作法如下：C₁是半径为a的圆，在C₁的圆内作四个相等的圆C₂（如图），每个圆C₂和圆C₁都内切，且相邻的两个圆C₂均外切，再在每一个圆C₂中，用同样的方法作四个相等的圆C₃，依此类推作出C₄，C₅，C₆，…，则
（1）圆C₂的半径长等于    （用a表示）；
（2）圆C_k的半径为    （k为正整数，用a表示，不必证明）

Answer 1

【答案】分析：（1）连接AB、BC、CD、AD，AC，设小圆的半径是r，根据圆与圆相切，得到AC=2a-2r，根据正方形的性质和勾股定理得到AC=2r，推出方程2a-2r=2r，求出即可；
（2）求出r=（-1）a，r₃=（-1）r=a，r₄=，得出圆C_k的半径为r_k=（-1 ）^k-1 a即可．
解答：（1）解：连接AB、BC、CD、AD，AC，
设小圆的半径是r，
根据圆与圆相切，
∴AC=2a-2r，
∴四边形ABCD是正方形，
∴AB=BC，∠B=90°，
由勾股定理得：AC=2r，
∴2a-2r=2r，
解得：r=（-1）a，
故答案为：（-1）a．

（2）解：由（1）得：r=（-1）a，
同理圆C₃的半径是r₃=（-1）r=a，
C₄的半径是r₄=，
…
圆C_k的半径为r_k=（-1 ）^k-1 a，
故答案为：r_k=（-1 ）^k-1 a．
点评：本题主要考查对正方形的性质和判定，勾股定理，相切两圆的性质等知识点的理解和掌握，能根据计算结果得出规律是解此题的关键．