题目内容
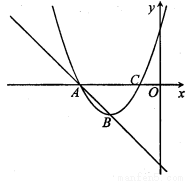
如图,已知A(-4, ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y= (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。

(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
(1)-4<x<-1;(2)y= ;m=-2.
;m=-2.
【解析】
试题分析:(1)根据图示直接得出答案;(2)将A、B两点坐标代入一次函数解析式求出k和b的值,将点B的坐标代入反比例函数解析式求出m的值;(3)首先根据一次函数设出点P的坐标,求出AC、OC、BD、OD的长度,根据△PCA和△PDB的面积相等列出关于x的方程求出x的值,然后得出点P的坐标.
试题解析:(1)由图象,当-4<x<-1时,一次函数值大于反比例函数的值。
(2)把A(-4, ),B(-1,2)代入y=kx+b得,
),B(-1,2)代入y=kx+b得, 解得:
解得:
∴ 一次函数的解析式为y=
把B(-1,2)代入y= 得m=-2,即m的值为-2。
得m=-2,即m的值为-2。
(3)设P的坐标为(x, ),由A、B的坐标可知AC=
),由A、B的坐标可知AC= ,OC=4,BD=1,OD=2,
,OC=4,BD=1,OD=2,
易知△PCA的高为x+4,△PDB的高2-( ),由
),由 可得
可得
 ,解得
,解得 ,此时
,此时
∴ P点坐标为( ,
, )
)
考点:一次函数与反比例函数的综合题.
考点分析: 考点1:反比例函数 一般地,函数 (k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
(k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。 注:
(1)因为分母不能为零,所以反比例函数函数的自变量x不能为零,同样y也不能为零;
(2)由
 ,所以反比例函数可以写成
,所以反比例函数可以写成 的形式,自变量x的次数为-1;
的形式,自变量x的次数为-1; (3)在反比例函数中,两个变量成反比例关系,即
 ,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。表达式:
x是自变量,y是因变量,y是x的函数
 自变量的取值范围:
自变量的取值范围:①在一般的情况下,自变量x的取值范围可以是不等于0的任意实数;
②函数y的取值范围也是任意非零实数。 反比例函数性质:
①反比例函数的表达式中,等号左边是函数值y,等号右边是关于自变量x的分式,分子是不为零的常数k,分母不能是多项式,只能是x的一次单项式;
②反比例函数表达式中,常数(也叫比例系数)k≠0是反比例函数定义的一个重要组成部分;
③反比例函数
 (k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
试题属性
(k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
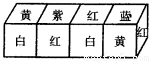
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况列表如下:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 6 | 5 | 4 | 3 | 2 | 1 |
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如下图所示,那么长方体的下底面共有______朵花.
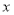 元,可得方程 .
元,可得方程 . 的顶点坐标是( )
的顶点坐标是( )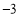 ) B、(
) B、(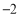 ,3) C、(2,3) D、(
,3) C、(2,3) D、(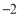 ,
,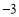 )
) 根的情况是( )
根的情况是( ) )·(
)·( -1),其中x=
-1),其中x=
 ÷x= ;
÷x= ;