题目内容
如图, 为⊙
为⊙ 的直径,
的直径, 与⊙
与⊙ 相切于点
相切于点 ,
, 与⊙
与⊙ 相切于点
相切于点 ,点
,点 为
为 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.

(1)求证: 为⊙
为⊙ 的切线;
的切线;
(2)若 ,求线段BC的长.
,求线段BC的长.
 为⊙
为⊙ 的直径,
的直径, 与⊙
与⊙ 相切于点
相切于点 ,
, 与⊙
与⊙ 相切于点
相切于点 ,点
,点 为
为 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.
(1)求证:
 为⊙
为⊙ 的切线;
的切线;(2)若
 ,求线段BC的长.
,求线段BC的长.(1)证明见解析;(2)BC= .
.
 .
.试题分析:(1)因为BC经过圆的半径的外端,只要证明AB⊥BC即可.连接OE、OC,利用△OBC≌△OEC,得到∠OBC=90°即可证明BC为⊙O的切线.
(2)作DF⊥BC于点F,构造Rt△DFC,利用勾股定理解答即可.
试题解析:(1)连接OE、OC.

∵CB=CE,OB=OE,OC=OC,
∴△OBC≌△OEC.
∴∠OBC=∠OEC.
又∵DE与⊙O相切于点E,
∴∠OEC=90°.
∴∠OBC=90°.
∴BC为⊙O的切线.
(2)过点D作DF⊥BC于点F,则四边形ABFD是矩形,BF=AD=2,DF=AB=2
 .
.∵AD、DC、BC分别切⊙O于点A、E、B,
∴DA=DE,CE=CB.
设BC为x,则CF=x﹣2,DC=x+2.
在Rt△DFC中,(x+2)2﹣(x﹣2)2=(2
 )2,解得x=
)2,解得x= .
.∴BC=
 .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目


 =2π,判断直线DC与⊙O的位置关系,并说明理由.
=2π,判断直线DC与⊙O的位置关系,并说明理由.

 90°,
90°, 3 cm,
3 cm, 4 cm,若⊙A,⊙B的半径分别为1 cm,4 cm,则⊙A,⊙B的位置关系是( )
4 cm,若⊙A,⊙B的半径分别为1 cm,4 cm,则⊙A,⊙B的位置关系是( )
 cm
cm cm
cm cm
cm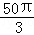 cm
cm


