题目内容
已知矩形ABCD中，对角线AC，BD相交于点0，AC=8，∠ACB=30°．则△AOB的周长是
- A.16
- B.12
- C.10
- D.8
B
分析：根据矩形的性质求出AO和BO的长，然后根据含30°的角的直角三角形的性质求出AB的长，三者相加即可求出答案．
解答：∵矩形ABCD中，对角线AC=8，
∴AO=BO=
AC=×8=4，
∵∠ACB=30°，
∴AB=AC=×8=4，
∴△AOB的周长=AO+BO+AB=4+4+4=12．
故选B．
点评：此题主要考查学生对矩形的性质和含30°的角的直角三角形的性质的理解和掌握，解答此题的关键是掌握矩形的对角线相等且互相平分．
分析：根据矩形的性质求出AO和BO的长，然后根据含30°的角的直角三角形的性质求出AB的长，三者相加即可求出答案．
解答：∵矩形ABCD中，对角线AC=8，
∴AO=BO=
AC=×8=4，∵∠ACB=30°，
∴AB=
AC=×8=4，∴△AOB的周长=AO+BO+AB=4+4+4=12．
故选B．
点评：此题主要考查学生对矩形的性质和含30°的角的直角三角形的性质的理解和掌握，解答此题的关键是掌握矩形的对角线相等且互相平分．
练习册系列答案
相关题目
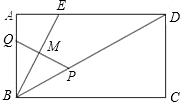
，点Q从点B以每秒1个单位沿BA方向向点A运动，设运动时间为t秒，△BPQ的面积为S．
如图，已知矩形ABCD中，BC=6，AB=8，延长AD到点E，使AE=15，连接BE交AC于点P．
如图：已知矩形ABCD中，CE∥DF．