Question

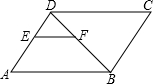
如图，E是平行四边形ABCD边CD的中点，连接AE、BD，交于点O．如果已知△ADE的面积是6，试写出能求出的图形面积    （要求写出四个以上图形的面积）．

Answer 1

【答案】分析：由于四边形ABCD是?，可得AB∥CD，再利用平行线分线段成比例定理，可得OE：OA=DE：AB，而E是CD中点，易求OE：OA的值，从而可求△AOD、△DOE，再利用相似三角形的面积比等于相似比的平方可求△AOB
的面积，也就易求△ABD的面积．
解答：解：如右图所示，
∵四边形ABCD是?，
∴AB∥CD，AB=CD，
∴OE：OA=DE：AB，
又∵DE=CE，
∴DE=AB，
∴OE：OA=1：2，
又S_△ADE=6，
∴S△_AOD=S_△ADE=4，
∴S_△DOE=2，
∴S_△AOB=4S_△DOE=8，
∴S_△ABD=4+8=12．
故答案为：S_△ODE=2，S_△ODA=4，S_△OBA=8，S_△ABD=12．
点评：本题考查了平行四边形的性质、平行线分线段成比例定理的推论、相似三角形的判定和性质，相似三角形的面积比等于相似比的平方、同高不同底的三角形的面积比等于底的比．