题目内容
【题目】如图所示,在梯形ABCD中,AB∥DC,BD⊥AD,AD=DC=BC=2cm,那么梯形ABCD的面积是 . 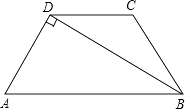
【答案】3 ![]() cm2
cm2
【解析】解:作DE⊥AB,垂足为E, 
∵AB∥DC,AD=DC=BC=2cm,
∴梯形ABCD为等腰梯形,△BCD为等腰三角形,
∴∠DAB=∠CBA,∠CDB=∠CBD,
又∵AB∥DC,
∴∠CDB=∠DBA,
∴∠CBD=∠DBA,
∴∠DBA= ![]() ∠CBA=
∠CBA= ![]() ∠DAB,
∠DAB,
设∠DBA=x,
∵DB⊥AD,
∴x+2x=90°,
解得x=30°,即∠DBA=30°,∠DAB=60°,
∴AB=4cm,
在Rt△ADE中,AE= ![]() AD=
AD= ![]() ×2=1cm,
×2=1cm,
DE= ![]() cm,
cm,
∴S梯形ABCD= ![]() =3
=3 ![]() cm2 .
cm2 .
所以答案是:3 ![]() cm2 .
cm2 .
【考点精析】通过灵活运用等腰梯形的性质,掌握等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等即可以解答此题.

练习册系列答案
相关题目