Question

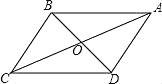
【题目】已知平行四边形ABCD中，如图，对角线AC和BD相交于点O，AC=10，BD=8．

（1）若AC⊥BD，试求四边形ABCD的面积；

（2）若AC与BD的夹角∠AOD=60°，求四边形ABCD的面积．

Answer 1

【答案】(1)S菱形ABCD＝40；(2)S四ABCD=20

【解析】

（1）先证平行四边形ABCD是菱形，根据菱形的面积公式即可求解；
（2）过点A分别作AE⊥BD，垂足为E，根据三角函数即可求得AE的长，从而求得△OAD的面积，四边形ABCD的面积是三角形OAD的面积的4倍，据此即可求解．

解：(1)∵AC⊥BD，

∴平行四边形ABCD为菱形，

∴S菱形ABCD＝AC×BD＝40；

(2)过点A分别作AE⊥BD，垂足为E，

∵四边形ABCD为平行四边形，

∴AO＝CO＝AC＝5，BO＝DO＝BD＝4，

在Rt△AOE中，sin∠AOE＝，

∴AE＝AOsin∠AOE＝AO×sin60°＝，

∴S四ABCD＝ODAE×4＝×4××4＝20．

故答案为：(1)S菱形ABCD＝40；(2)S四ABCD=20 .