题目内容
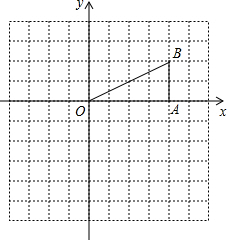 如图,Rt△OAB中,∠OAB=90°,B(4,2).
如图,Rt△OAB中,∠OAB=90°,B(4,2).(1)△OAB向下平移3个单位后得△O1A1B1,则A1的坐标为
(4,-3)
(4,-3)
;(2)△OAB绕点O顺时针旋转90°后得△OA2B2,则B2的坐标为
(2,-4)
(2,-4)
;(3)在图中画出△O1A1B1,△OA2B2,直接写出它们覆盖的面积为
| 9 |
| 20 |
| 9 |
| 20 |
分析:(1)根据网格结构找出点O、A、B向下平移3个单位的点O1、A1、B1的位置,然后顺次连接即可,再根据平面直角坐标系写出点A1的坐标;
(2)根据网格结构找出点A、B绕点O顺时针旋转90°后的对应点A2、B2的位置,然后顺次连接即可,再根据平面直角坐标系写出点B2的坐标;
(3)根据勾股定理列式求出OB2,然后利用∠A2OB2的正弦求出O1D,然后求出△OA2B2的面积,再根据相似三角形面积的比等于相似比的平方求解.
(2)根据网格结构找出点A、B绕点O顺时针旋转90°后的对应点A2、B2的位置,然后顺次连接即可,再根据平面直角坐标系写出点B2的坐标;
(3)根据勾股定理列式求出OB2,然后利用∠A2OB2的正弦求出O1D,然后求出△OA2B2的面积,再根据相似三角形面积的比等于相似比的平方求解.
解答: 解:(1)△O1A1B1如图所示,A1的坐标为(4,-3);
解:(1)△O1A1B1如图所示,A1的坐标为(4,-3);
(2)△OA2B2如图所示,B2的坐标为(2,-4);
(3)如图,根据勾股定理,OB2=
=2
,
O1D=OO1•sin∠A2OB2=3×
=
,
∵S△O1A1B1=
×4×2=4,
∴覆盖部分的面积=4×(
)2=4×
=
.
故答案为:(4,-3);(2,-4);
.
 解:(1)△O1A1B1如图所示,A1的坐标为(4,-3);
解:(1)△O1A1B1如图所示,A1的坐标为(4,-3);(2)△OA2B2如图所示,B2的坐标为(2,-4);
(3)如图,根据勾股定理,OB2=
| 22+42 |
| 5 |
O1D=OO1•sin∠A2OB2=3×
| 2 | ||
2
|
3
| ||
| 5 |
∵S△O1A1B1=
| 1 |
| 2 |
∴覆盖部分的面积=4×(
| ||||
| 4 |
| 9 |
| 80 |
| 9 |
| 20 |
故答案为:(4,-3);(2,-4);
| 9 |
| 20 |
点评:本题考查了利用旋转变换作图,利用平移变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键,(3)利用相似三角形面积的比等于相似比的平方求解比较简单.

练习册系列答案
相关题目
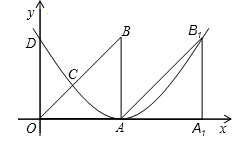 方向平移1个单位长度后得△AA1B1.
方向平移1个单位长度后得△AA1B1. (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.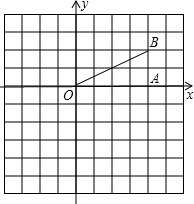 (1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;
(1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;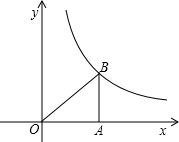 如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数
如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数