题目内容
【题目】
中，
，
于点
，
于点
，
为
边的中点，连结
，
，则下列结论：①
②
③
为等边三角形④若
，则
，则正确结论是________.
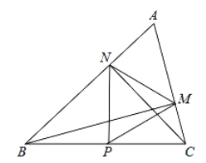
【答案】①②③④
【解析】
①根据直角三角形斜边上的中线等于斜边的一半可判断①正确；
②先证明△ABM∽△ACN，再根据相似三角形的对应边成比例可判断②正确；
③先根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°，再根据三角形的内角和定理求出∠BCN+∠CBM=60°，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°，从而得到∠MPN=60°，又由①得PM=PN，根据有一个角是60°的等腰三角形是等边三角形可判断③正确；
④根据P为BC边的中点得出
，求出∠ABC，根据三角形的内角和定理求出∠ACB即可可判断④正确．
解：①
于点
，
于点
，
为
边的中点，
，
，
，故①正确；
②在
与
中，
，
，
，
，
，故②正确；
③
，于点，于点，
，
在
中，
，
点是的中点，，，
，
，
，
，
，
是等边三角形，故③正确；
，
（为的中点），
，
，
，
，
，故④正确；
故答案为：①②③④.
练习册系列答案
相关题目
