题目内容
【题目】△ABC中,∠C=60°,点D,E分别是边AC,BC上的点,点P是直线AB上一动点,连接PD,PE,设∠DPE=α.
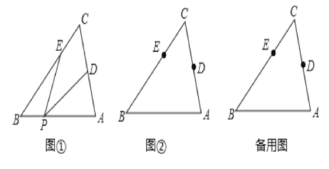
(1)如图①所示,如果点P在线段BA上,且α=30°,那么∠PEB+∠PDA=___;
(2)如图②所示,如果点P在线段BA上运动,
①依据题意补全图形;
②写出∠PEB+∠PDA的大小(用含α的式子表示);并说明理由。
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是___.
【答案】(1)90°;(2)①见解析,②60°α;(3)60°+α或60°α或60°;
【解析】
(1)连接PC,由三角形的外角性质即可得出结论;
(2)①根据题意画出图形即可;
②由三角形的外角性质即可得出结论;
(3)分三种情况讨论,由三角形的外角性质即可得出结论.
;(1)∠PEB+∠PDA=90;理由如下;
连接PC,如图1所示
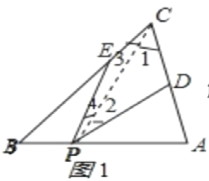
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+30°=90
故答案为:90°;
(2)①如图2所示;
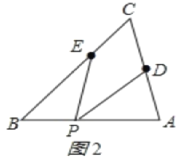
②连接PC,如图3所示:
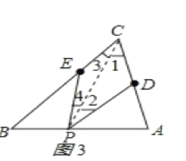
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角,
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+α;
∴∠PEB+∠PDA=60°+α;
(3)分三种情况:
①如图4所示:
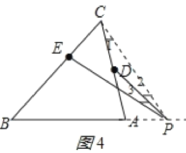
连接PC,
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2+∠3,∠PDA=∠1+∠2
∴∠PEB∠PDA=∠ACB+∠3=60°+α;
②如图5所示:连接PC,
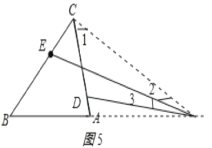
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2+∠3
∴∠PEB∠PDA=∠ACB∠3=60°α;
③如图6所示:P、D. E在同一条直线上,连接PC,
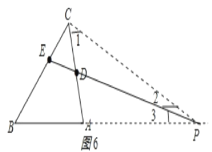
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2,
∴∠PEB∠PDA=∠ACB=60°;
综上所述:如果点P在线段BA的延长线上运动,
∠PEB与∠PDA之间的数量关系是60°+α或60°α或60°;
故答案为:60°+α或60°α或60°.







