题目内容
函数y=x+1与坐标轴围成的三角形的面积是
．
| 1 |
| 2 |
| 1 |
| 2 |
分析：先令x=0求出y的值，再令y=0求出x的值，即可得出直线与两坐标轴的交点．再由三角形的面积公式即可得出结论．
解答：解：∵令x=0，则y=1；y=0，则x=-1，
∴函数y=x+1与x轴的交点为（-1，0），与y轴的交点为（0，1），
∴函数y=x+1与坐标轴围成的三角形的面积=
×1×1=
．
故答案为：
．
∴函数y=x+1与x轴的交点为（-1，0），与y轴的交点为（0，1），
∴函数y=x+1与坐标轴围成的三角形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查的是一次函数图象上点的坐标特点，即一次函数图向上各点的坐标一定适合此函数的解析式．
练习册系列答案
相关题目
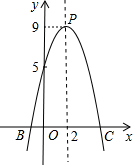二次函数的图象如图所示，P为图象顶点，A为图象与y轴交点．
称轴是x=1，如图为函数图象的一部分．
（2012•玄武区一模）已知二次函数y=-x2+（m-1）x+m．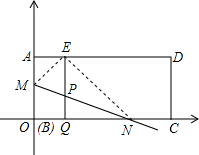
D上的E处（若折痕MN与x轴相交时，其交点即为N），过点E作EQ⊥BC于Q，交折痕于点P．