Question

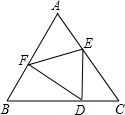△ABC为等边三角形，且DE⊥BC，垂足为D，EF⊥AC，垂足为E，FD⊥AB，垂足为F，则△DEF是等边三角形吗？为什么？

Answer 1

解：△DEF是等边三角形．理由如下：
∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，
∵DE⊥BC，EF⊥AC，FD⊥AB，
∴∠AEF=∠BFD=∠CDE=90°，
∴∠AFE=∠BDF=∠CED=30°，
∴∠FED=∠EDF=∠DFE=60°，
∴△DEF是等边三角形．
分析：根据等边三角形的性质由△ABC为等边三角形得∠A=∠B=∠C=60°，再利用垂直的定义得到∠AEF=∠BFD=∠CDE=90°，根据三角形内角和定理可得∠AFE=∠BDF=∠CED=30°，然后根据平角的定义得∠FED=∠EDF=∠DFE=60°，最后根据等边三角形的判定方法得到△DEF是等边三角形．
点评：本题考查了等边三角形的判定与性质：等边三角形的三条边相等，三个内角都等于60°；有两个内角都等于60°的三角形为等边三角形．