Question

【题目】在△ABC中，∠ABC＝60°，∠ACB＝70°，若点O到三边的距离相等，则∠BOC＝_____°．

Answer 1

【答案】115或65或22.5

【解析】

先画出符合的图形，再根据角平分线的性质和三角形的内角和定理逐个求出即可．

解：①如图，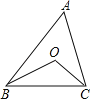

∵点O到三边的距离相等，

∴点O是△ABC的三角的平分线的交点，

∵∠ABC＝60°，∠ACB＝70°，

∴∠OBC＝∠ABC＝30°，∠ACB＝35°，

∴∠BOC＝180°﹣∠OBC﹣∠OCB＝115°；

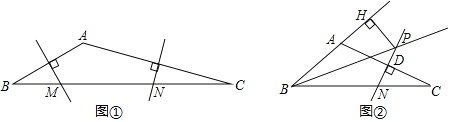
②如图，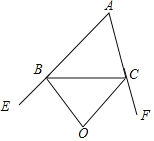

∵∠ABC＝60°，∠ACB＝70°，

∴∠EBC＝180°﹣∠ABC＝120°，∠FCB＝180°﹣∠ACB＝110°，

∵点O到三边的距离相等，

∴O是∠EBC和∠FCB的角平分线的交点，

∴∠OBC＝∠EBC＝60°，∠FCB＝55°，

∴∠BOC＝180°﹣∠OBC﹣∠OCB＝65°；

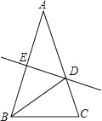
③如图，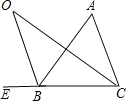

∵∠ABC＝60°，∠ACB＝75°，

∴∠A＝180°﹣∠ABC﹣∠ACB＝45°，

∵点O到三边的距离相等，

∴O是∠EBA和∠ACB的角平分线的交点，

∴∠OBA＝∠EBA＝×（180°﹣60°）＝60°，∠ACB＝37.5°，

∴∠BOC＝180°﹣（∠OBA+∠ABC+∠OCB）＝180°﹣（60°﹣60°﹣37.5°）＝22.5°；

如图，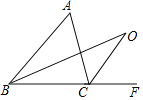

此时∠BOC＝22.5°，

故答案为：115或65或22.5．