题目内容
 (1)计算:|-1|+
(1)计算:|-1|+
 +(-3.14)0-(
+(-3.14)0-( )-1.
)-1.
(2)解方程:2x2-6x-1=0.
(3)如图,在平行四边形ABCD中,E为BC中点,AE和延长线与DC的延长线相交于点F.证明:△ABE≌△FCE.
解:(1)原式=1+ +1-2
+1-2
= ;
;
(2)∵2x2-6x-1=0,
∴x2-3x= ,
,
∴x2-3x+ =
= +
+ .
.
∴(x- )2=
)2= ,
,
∴x- =±
=±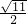 ,
,
∴x1= ,x2=
,x2=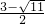 ;
;
(3)证明:∵四边形ABCD是平行边形,
∴AB∥CD,
∴∠EAB=∠F,
∵E是BC中点,
∴BE=CE,
∵在△ABE和△FCE中,
 ,
,
∴△ABE≌△FCE(AAS).
分析:(1)由二次根式的化简,零指数幂与负指数幂的性质以及绝对值的性质,即可求得答案;
(2)利用配方法求解即可求得答案;
(3)由四边形ABCD是平行四边形,可得AB∥CD,又由E为BC中点,即可证得:△ABE≌△FCE.
点评:此题考查了平行四边形的性质、一元二次方程的解法以及实数的运算.此题难度不大,注意掌握数形结合思想的应用.
 +1-2
+1-2=
 ;
;(2)∵2x2-6x-1=0,
∴x2-3x=
 ,
,∴x2-3x+
 =
= +
+ .
.∴(x-
 )2=
)2= ,
,∴x-
 =±
=±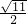 ,
,∴x1=
 ,x2=
,x2=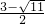 ;
;(3)证明:∵四边形ABCD是平行边形,
∴AB∥CD,
∴∠EAB=∠F,
∵E是BC中点,
∴BE=CE,
∵在△ABE和△FCE中,
 ,
,∴△ABE≌△FCE(AAS).
分析:(1)由二次根式的化简,零指数幂与负指数幂的性质以及绝对值的性质,即可求得答案;
(2)利用配方法求解即可求得答案;
(3)由四边形ABCD是平行四边形,可得AB∥CD,又由E为BC中点,即可证得:△ABE≌△FCE.
点评:此题考查了平行四边形的性质、一元二次方程的解法以及实数的运算.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
