题目内容
如图，在同一平面内，将两个全等的等腰直角
和
摆放在一起，
为公共顶点，
，它们的斜边长为2，若固定不动，绕点旋转，
、
与边
的交点分别为
、
（点不与点
重合，点不与点
重合），设
，
.
（1）请在图中找出两对相似而不全等的三角形，并选取其中一对加以证明.
（2）求
与
的函数关系式，直接写出自变量的取值范围.
（1）证明略
（2）
，或
（
）
解析:（1）
∽
,
∽.
证明：∵
和
是全等的等腰直角三角形，且
，
∴
， 又∵
（公共角），
∴∽. 同理可证∽.
（2）由（1）可知∽,∽，则有∽.
∴
又∵是等腰直角三角形，且
，
∴
，又
，
，
∴
，即，或（）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20、如图，在同一平面内，有三条直线a、b、c，且a∥b，如果直线a与c交于点O，那么直线c与b的位置关系是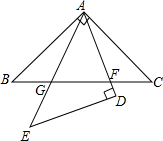
如图，在同一平面内，将两个全等的等腰直角三角形ABC和ADE摆放在一起，A为公共顶点，∠BAC=∠ADE=90°，若△ABC固定不动，△ADE绕点A旋转，AD、AE与边BC的交点分别为F、G（点G不与点B重合，点F不与点C重合）．
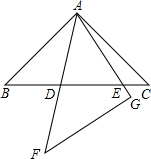点分别为D、E（点D不与点B重合，点E不与点C重合），设BE=m，CD=n．
按要求作图：
如图，在同一平面内有A、B、C三个点，根据要求画图：