题目内容
把下列各数填在相应的大括号里：（漏选或少选均不给分）
，
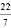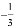，-12，-1.04，
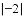，+5，-（-3），3.1415，-8
正数集合{ …}
分数集合{ …}
负整数集合{ …}
负有理数集合{ …}
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
快乐暑假暑假能力自测中西书局系列答案题目内容
把下列各数填在相应的大括号里：（漏选或少选均不给分）
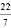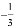，，-12，-1.04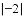，，+5，-（-3），3.1415，-8
正数集合{ …}
分数集合{ …}
负整数集合{ …}
负有理数集合{ …}
快乐暑假暑假能力自测中西书局系列答案
，且经过点（2，0），下列说法：①abc＜0；②﹣2b+c=0；③4a+2b+c＜0；④若(
，y1)、(
，y2)是抛物线上的两点，则y1＜y2；⑤
>m(am+b)（其中m≠
x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y=
x2+bx+c经过点B，与直线l的另一个交点为C（4，n）．
________－
（填“>、<或=”）．