题目内容
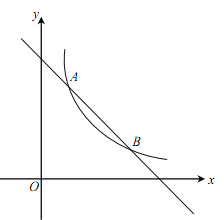
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
【答案】(1)![]() ,
,![]() ;(2)P
;(2)P ![]() ,
,![]() .
.
【解析】
试题分析:(1)把A的坐标代入一次函数可得到a的值,从而得到k的值,联立一次函数和反比例函数成方程组,解方程组即可得到点B的坐标;
(2)作B关于x轴的对称点![]() ,连接
,连接![]() 交x轴于点
交x轴于点![]() ,连接
,连接![]() ,则有,
,则有, ![]() ,当P点和
,当P点和![]() 点重合时取到等号.求得直线
点重合时取到等号.求得直线![]() 的解析式,进而求出
的解析式,进而求出![]() ,即满足条件的P的坐标为
,即满足条件的P的坐标为![]() ,设
,设![]() 交x轴于点C,则
交x轴于点C,则![]() ,由
,由![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)由已知可得,![]() ,
,![]() ,∴反比例函数的表达式为
,∴反比例函数的表达式为![]() ,联立
,联立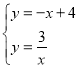 ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ;
;
(2)如答图所示,把B点关于x轴对称,得到![]() ,连接
,连接![]() 交x轴于点
交x轴于点![]() ,连接
,连接![]() ,则有,
,则有, ![]() ,当P点和
,当P点和![]() 点重合时取到等号.易得直线
点重合时取到等号.易得直线![]() :
:![]() ,令
,令![]() ,得
,得![]() ,∴
,∴![]() ,即满足条件的P的坐标为
,即满足条件的P的坐标为![]() ,设
,设![]() 交x轴于点C,则
交x轴于点C,则![]() ,∴
,∴![]() ,即
,即![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目