Question

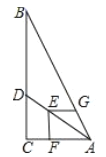
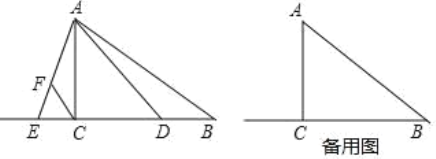
【题目】已知，如图，Rt△ABC 中，∠ACB=90°，BC=8，AC=6，点 D 在边 BC 上（不 与点 B、C 重合），点 E 在边 BC 的延长线上，∠DAE=∠BAC，点 F 在线段 AE 上，∠ACF=∠B．设 BD=x．

（1）若点 F 恰好是 AE 的中点，求线段 BD 的长；

（2）若 y=，求 y 关于 x 的函数关系式，并写出它的定义域；

（3）当△ADE 是以 AD 为腰的等腰三角形时，求线段 BD 的长．

Answer 1

【答案】（1）；（2）；（3）或

【解析】

（1）先判断出△ABD∽△ACF，进而判断出AD=BD，再用解直角三角形的方法即可得出BD；
（2）先表示出CF，进而表示出MC，即可得出函数关系式；
（3）分两种情况列出方程求解即可得出结论．

解：（1）在中，，，，

∴，

∵，

∴，

∵，

∴，

∴，

在中，点恰好是的中点，

∴，

∴

在中，，，根据勾股定理得，，

∴，

∴，

∴，

（2）如图1，过点作于M，由（1）知，

∴，

∴，

由（1），

∴，

∴，

∴，

∴

（3）∵是以AD为腰的等腰三角形，

当AD=AE时，

∵，

∴，

∴，

∴是的平分线，

∴，

∵，

∴，

∴，

当时，

∵，

∴，

∴∠B=∠DAB，

∴

综上所述当或时，是以为腰的等腰三角形．