Question

【题目】（1）作图发现：

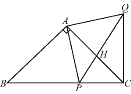
如图1，已知，小涵同学以、为边向外作等边和等边，连接，．这时他发现与的数量关系是 ．

（2）拓展探究：

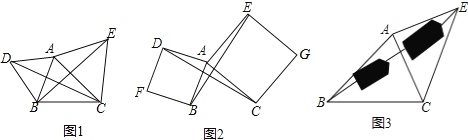
如图2，已知，小涵同学以、为边向外作正方形和正方形，连接，，试判断与之间的数量关系，并说明理由．

（3）解决问题

如图3，要测量池塘两岸相对的两点，的距离，已经测得，，米，，则 米．

Answer 1

【答案】（1）BE=CD；（2）BE=CD，理由见解析；（3）200．

【解析】

（1）利用等边三角形的性质得出，然后有，再利用SAS即可证明，则有；

（2）利用正方形的性质得出，然后有，再利用SAS即可证明，则有；

（3）根据前（2）问的启发，过作等腰直角，连接，，同样的方法证明，则有，在中利用勾股定理即可求出CD的值，则BE的值可求．

（1）如图1所示：

和都是等边三角形，

，

，

即，

在和中，

，

．

（2），

四边形和均为正方形，

，，，

，

在和中，

，

，

（3）如图3，

过作等腰直角，，

则米，，

米，

连接，，

∴

即

在和中，

，

，

，

，

在中，米，米，

根据勾股定理得：（米），

则米．