题目内容
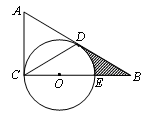
如图,AB是⊙O的直径,C是 的中点,CE⊥AB于E,BD交CE于点F,
的中点,CE⊥AB于E,BD交CE于点F,
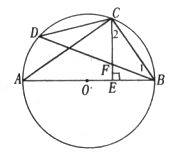
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长。
 的中点,CE⊥AB于E,BD交CE于点F,
的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长。
(1)证明见解析;(2)10,9.6.
试题分析:(1)由AB是⊙O的直径,CE⊥AB,易得∠2=∠A,又由C是
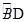 的中点,可得∠1=∠A,即可得∠1=∠2,判定CF=BF;
的中点,可得∠1=∠A,即可得∠1=∠2,判定CF=BF;(2)由C是
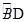 的中点,可得BC=CD=12,又由AB是⊙O的直径,可得∠ACB=90°,即可求得AB的长,然后由三角的面积,求得CE的长.
的中点,可得BC=CD=12,又由AB是⊙O的直径,可得∠ACB=90°,即可求得AB的长,然后由三角的面积,求得CE的长.试题解析:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠CEB=90°,
∴∠2=90°-∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,
∴∠1=∠2,
∴CF=BF;
(2)∵C是
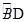 的中点,
的中点,∴
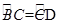 ,
,∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,
∴⊙O的半径为10,
∵S△ABC=
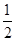 AC•BC=
AC•BC=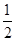 AB•CE,
AB•CE,∴
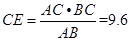 .
.考点: 1.圆周角定理;2.勾股定理;3.圆心角、弧、弦的关系.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 和根号).
和根号).