题目内容
如图，一块五边形木板ABCDE是由矩形木板AFDE截去∠F后剩下的，AE=130cm，ED=100cm，BF=80cm，FC=40cm．现要在五边形木板ABCDE上再截一块矩形木板NPME，且点P在线段BC上，若设PM的长为x（cm），矩形NPME的面积为y（cm2）．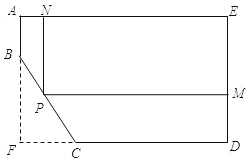
求：（1）y与x的函数关系式，并写出x的取值范围；
（2）求当x为何值时，面积y最大，最大面积为多少？
分析：（1）设PM=x，表示PN的长，为此延长NP交FD于点H，构造△CPH∽△CBF，利用对应边的比相等可求PH，PN=NH-PH=100-PH，根据题意求出自变量x的范围；
（2）根据矩形面积公式求函数y，根据抛物线对称轴及自变量x的范围求最大值．
（2）根据矩形面积公式求函数y，根据抛物线对称轴及自变量x的范围求最大值．
解答：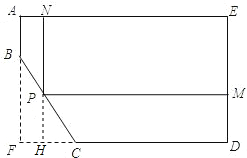
解：（1）延长NP交FD于点H，
CH=HD-CD=PM-（FD-FC）
=x-（130-40）=x-90
∵PH∥BF，
∴△CPH∽△CBF．
∴
=
．
即
=
．
∴PH=2x-180．
则y=PM•EM=x•[100-（2x-180）]=-2x2+280x
90≤x≤130．
（2）∵90≤x≤130
又因为抛物线y=-x2+220x的对称轴为x=70，开口向下．
所以，在90≤x≤130内y随x的增大而减小，
当x=90时，y=-2x2+280x取得最大值．
其最大值为y=9000cm2．
解：（1）延长NP交FD于点H，CH=HD-CD=PM-（FD-FC）
=x-（130-40）=x-90
∵PH∥BF，
∴△CPH∽△CBF．
∴
| PH |
| BF |
| CH |
| CF |
即
| PH |
| 80 |
| x-90 |
| 40 |
∴PH=2x-180．
则y=PM•EM=x•[100-（2x-180）]=-2x2+280x
90≤x≤130．
（2）∵90≤x≤130
又因为抛物线y=-x2+220x的对称轴为x=70，开口向下．
所以，在90≤x≤130内y随x的增大而减小，
当x=90时，y=-2x2+280x取得最大值．
其最大值为y=9000cm2．
点评：本题结合表示矩形PMEN的面积考查二次函数的综合应用，注意在设矩形一边长后，求另一边长，把问题转化到相似三角形来解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
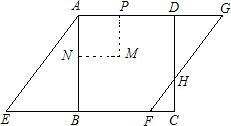EF的中点．由于受木料纹理的限制，要求裁出的矩形要以点A为一个顶点．
