题目内容
(1)如图1,△ABC中,∠A=60°,∠B:∠C=1:5,求∠B的度数.
(2)如图2,点M为正方形ABCD对角线BD上一点,分别连接AM、CM.求证:AM=CM.

(1)解:∵∠A+∠B+∠C=180°,∠A=60°,
∴∠B+∠C=180°-60°=120°,
∵∠B:∠C=1:5,
∴∠B+5∠B=120°,
∴∠B=20°;
(2)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABM=∠CBM,
∵BM是公共边,
∴△ABM≌△CBM,
∴AM=CM.
分析:(1)由三角形的内角和定理以及已知条件可求得∠B;
(2)根据正方形的性质,得AB=CB,∠ABM=∠CBM,则△ABM≌△CBM,则AM=CM.
点评:本题考查了全等三角形的判定和性质、正方形的性质以及三角形的内角和定理,是基础知识要熟练掌握.
∴∠B+∠C=180°-60°=120°,
∵∠B:∠C=1:5,
∴∠B+5∠B=120°,
∴∠B=20°;
(2)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABM=∠CBM,
∵BM是公共边,
∴△ABM≌△CBM,
∴AM=CM.
分析:(1)由三角形的内角和定理以及已知条件可求得∠B;
(2)根据正方形的性质,得AB=CB,∠ABM=∠CBM,则△ABM≌△CBM,则AM=CM.
点评:本题考查了全等三角形的判定和性质、正方形的性质以及三角形的内角和定理,是基础知识要熟练掌握.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图,如果AB∥CD,那么下面说法错误的是( )
如图,如果AB∥CD,那么下面说法错误的是( ) 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF. 如图,直线AB、CD被直线CE所截.
如图,直线AB、CD被直线CE所截.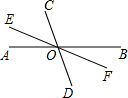 如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( )
如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( ) 如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.
如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.