题目内容
某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第n棵树种植在点Pn(xn,yn)处,其中x1=1,y1=1,当n≥2时,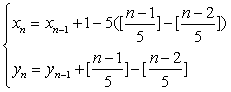 ,[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点的坐标为( )
,[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点的坐标为( )
A.(4,2010) B.(5,2009) C.(4,402) D.(5,401)
C.
详解:当n=1时,P1=(1,1);
当2≤n≤5时,P2,P3,P4,P5的坐标分别为(2,1)、(3,1)、(4,1)、(5,1);
当n=6时,P6=(1,2);
当7≤n≤10时,P7,P8,P9,P10的坐标分别为(2,2)、(3,2)、(4,2)、(5,2);
当n=11时,P11=(1,3);
当12≤n≤15时,P12,P13,P14,P15的坐标分别为(2,3)、(3,3)、(4,3)、(5,3)…
通过以上数据可以得出:当n=1+5x时,Pn的坐标为(1,x+1),而后面四个点的纵坐标均为x+1,横坐标则分别为2,3,4,5.因为2009=1+5×401+3,所以P2009的横坐标为4,纵坐标为402.故本题选C.

练习册系列答案
相关题目
 ,那么袋中的球共有__________个.
,那么袋中的球共有__________个. ,整体鱼向右移动了两个单位
,整体鱼向右移动了两个单位
 0),(4,2),(0,0),在下面的平面直角坐标系A中描出,并将点顺次连接.
0),(4,2),(0,0),在下面的平面直角坐标系A中描出,并将点顺次连接.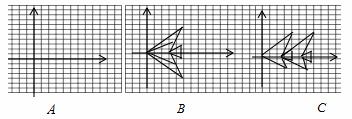
 B.
B.  C.
C. 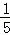 D.
D. 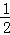
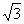
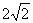 D.
D.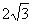
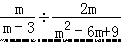 ,其中 m=1.
,其中 m=1.