题目内容
已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC.
(1) 求证:∠ABE=∠C;
(2) 若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=6,AC=10,求DC的长;
(3) 若BE平分∠ABC,AF平分∠BAC,且FD∥BC交AC于点D,连接FC,则△DFC是什么三角形?为什么?

(1)证明:∵ ∠AEB=∠ABC,
且∠AEB=∠EBC+∠C,∠ABC=∠EBC+∠ABE,
∴ ∠EBC+∠C=∠EBC+∠ABE,
∴ ∠ABE=∠C;
 (2)解: ∵ ∠BAE的平分线AF交BE于F,
(2)解: ∵ ∠BAE的平分线AF交BE于F,
∴ ∠BAF=∠DAF,
∵ FD∥BC交AC于D,
∴ ∠ADF=∠C,
∵ ∠ABE=∠C,
∴ ∠ADF=∠ABE,即∠ADF=∠ABF,
∵ AF=AF,
AF=AF,
∴ △BAF≌△DAF,
∴ AD=AB=6,
∴ DC=AC-AD=10-6=4.
(3)解: △DFC是等腰三角形.理由是:
过点F分别作FH⊥AB,FN⊥BC,FM⊥AC,
易证:
△AFH≌△AFM(AAS),从而知FH=FM,
△BFH≌△BFM(AAS),从而知FH=FN,
∴FM=FN,又FC=FC,可证Rt△CFM≌Rt△CFN(HL)
∴∠MCF=∠NCF,
∵FD∥BC,
∴∠DFC=∠BCF,
∴∠DFC=∠MCF,
∴DF=DC,
∴△DFC是等腰三角形.

 ,则
,则 ____________.
____________.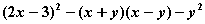 ,其中
,其中 .
. 的倒数是学 ( )
的倒数是学 ( ) D、
D、

 -3.8,0,﹣8, ,(-3)2,
-3.8,0,﹣8, ,(-3)2, 

