Question

【题目】在菱形中，．

（1）如图1，点为线段的中点，连接，．若，求线段的长．

（2）如图2，为线段上一点（不与，重合），以为边向上构造等边三角形，线段与交于点，连接，，为线段的中点．连接，判断与的数量关系，并证明你的结论．

（3）在（2）的条件下，若，请你直接写出的最小值．

Answer 1

【答案】（1）EC=；（2）DM=2DQ；（3）DM+CN的最小值为2．

【解析】

（1）如图1，连接对角线BD，先证明△ABD是等边三角形，根据E是AB的中点，由等腰三角形三线合一得：DE⊥AB，利用勾股定理依次求DE和EC的长；

（2）如图2，作辅助线，构建全等三角形，先证明△ADH是等边三角形，再由△AMN是等边三角形，得条件证明△ANH≌△AMD（SAS），则HN=DM，根据DQ是△CHN的中位线，得HN=2DQ，由等量代换可得结论．

（3）先判断出点N在CD的延长线上时，CN+DM最小，最小为CH，再判断出∠ACD=30°，即可用三角函数求出结论．

解：（1）如图1，

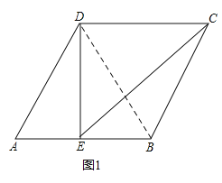
连接BD，则BD平分∠ABC，

∵四边形ABCD是菱形，

∴AD∥BC，

∴∠A+∠ABC=180°，

∵∠A=60°，

∴∠ABC=120°，

∴∠ABD=∠ABC=60°，

∴△ABD是等边三角形，

∴BD=AD=4，

∵E是AB的中点，

∴DE⊥AB，

由勾股定理得：DE=，

∵DC∥AB，

∴∠EDC=∠DEA=90°，

在Rt△DEC中，DC=4，

EC=；

（2）如图2，

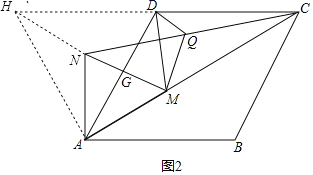
延长CD至H，使DH=CD，连接NH、AH，

∵AD=CD，

∴AD=DH，

∵CD∥AB，

∴∠HDA=∠BAD=60°，

∴△ADH是等边三角形，

∴AH=AD，∠HAD=60°，

∵△AMN是等边三角形，

∴AM=AN，∠NAM=60°，

∴∠HAN+∠NAG=∠NAG+∠DAM，

∴∠HAN=∠DAM，

在△ANH和△AMD中，

∴△ANH≌△AMD（SAS），

∴HN=DM，

∵D是CH的中点，Q是NC的中点，

∴DQ是△CHN的中位线，

∴HN=2DQ，

∴DM=2DQ．

（3）如图2，由（2）知，HN=DM，

∴要CN+DM最小，便是CN+HN最小，

即：点C，H，N在同一条线上时，CN+DM最小，

此时，点D和点Q重合，

即：CN+DM的最小值为CH，

如图3，

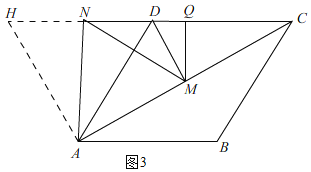
由（2）知，△ADH是等边三角形，

∴∠H=60°．

∵AC是菱形ABCD的对角线，

∴∠ACD=∠BCD=∠BAD=30°，

∴∠CAH=180°-30°-60°=90°，

在Rt△ACH中，CH==2，

∴DM+CN的最小值为2．