题目内容
如图，AB⊥BD，CD⊥BD，AB=6，CD=16，BD=20，一动点P从B向D运动，问当P离B多远时，△PAB与△PCD是相似三角形？试求出所有符合条件的P点的位置．
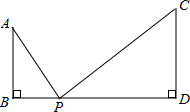
设BP=x，BD=20，则PD=BD-BP=20-x，
分两种情况考虑：
假设△PAB∽△PCD，有
=
，
又AB=6，CD=16，
∴
=
，即6（20-x）=16x，
解得：x=
；
假设△PAB∽△CPD，有
=
，
∴
=
，即x（20-x）=96，
整理得：（x-12）（x-8）=0，
解得：x1=12，x2=8，
综上，当P离B的距离为
或8或12时，△PAB与△PCD是相似三角形．
分两种情况考虑：
假设△PAB∽△PCD，有
| AB |
| CD |
| BP |
| DP |
又AB=6，CD=16，
∴
| 6 |
| 16 |
| x |
| 20-x |
解得：x=
| 60 |
| 11 |
假设△PAB∽△CPD，有
| AB |
| PD |
| BP |
| CD |
∴
| 6 |
| 20-x |
| x |
| 16 |
整理得：（x-12）（x-8）=0，
解得：x1=12，x2=8，
综上，当P离B的距离为
| 60 |
| 11 |
练习册系列答案
名校课堂系列答案
相关题目
