Question

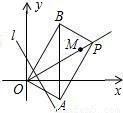
如图，平面上一点P从点M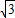（，1）出发，沿射线OM方向以每秒1个单位长度的速度作匀速运动，在运动过程中，以OP为对角线的矩形OAPB的边长OA：OB=1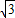：；过点O且垂直于射线OM的直线l与点P同时出发，且与点P沿相同的方向、以相同的速度运动．
（1）在点P运动过程中，试判断AB与y轴的位置关系，并说明理由．
（2）设点P与直线l都运动了t秒，求此时的矩形OAPB与直线l在运动过程中所扫过的区域的重叠部分的面积S．（用含t的代数式表示）

Answer 1

【答案】分析：（1）证AB与y轴平行，可根据OA：OB的值得出特殊角的度数，然后利用矩形的性质：对角线互相平分且相等，得出∠MOB=∠ABO=30°，根据M点的坐标可得出∠MOS=30°，即∠BOS=60°由此可证得AB⊥x轴即AB∥y轴．
（2）先找出关键时刻的t的值．OM=2，因此PO=2+t．
当l与AD重合时，此时OC=OD=t，即t=OA=OP=（2+t）
当l与BE重合时，OC=OE=t，EP=OD=（2+t），因此OE=t=（2+t）
因此本题可分三种情况进行讨论：
①当0＜t≤（2+t），即0＜t≤时，此时直线l在OD上运动，扫过部分是个直角三角形，此时OC=t，易求得直角三角形的两条直角边分别为t和2t，由此可求出扫过部分的面积．
②当（2+t）＜t≤（2+t），即＜t≤6时，扫过部分是个直角梯形．可根据CE的长求出梯形的上底，进而求出梯形的面积．
③当t＞（2+t）即t＞6时，重合部分是个多边形，可用矩形的面积减去右边的小三角形的面积进行求解．
解答：解：（1）AB∥y轴．
理由：∵Rt△OAB中，tan∠ABO=OA：OB=1：，
∴∠ABO=30°，
设AB交OP于点Q，交x轴于点S，
∵矩形的对角线互相平分且相等，则QO=QB，
∴∠QOB=30°，
过点M作MT⊥x轴于T，则tan∠MOT=1：，
∴∠MOT=30°，
∴∠BOS=60°，
∴∠BSO=90°，
∴AB∥y轴；

（2）过点A作垂直于射线OM的直线交OM于点D，过点B且垂直于射线OM的直线交OM于点E，

则OD=t．
∵OP=2+t，
∴OB=（2+t），OE=（2+t），OA=（2+t），OD=（2+t），
①当0＜t≤（2+t），即0＜t≤时，S=t²，
②当（2+t）＜t≤（2+t）即＜t≤6时，
设直线l交OB于F，交PA于G，交OP于点C，
则OF=t，PG=CP=，
∴AG=PA-=t-，S=（t-+t）•（2+t）=t²+t-．
③当t＞（2+t）即t＞6时，
∵CP=2，
∴S=S_矩形-×4×=（2+t）×（2+t）-=t²+t-．
点评：本题是运动性问题，考查了矩形的性质和图形面积的求法，找出几个关键点是解题的关键．