题目内容
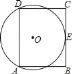
【题目】如图:![]() 是
是![]() 的直径,
的直径,![]() 是弦,
是弦,![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() .
.
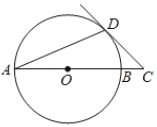
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接DO,由三角形的外角与内角的关系可得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.
(2)由(1)可得![]() OCD是等腰直角三角形,再根据勾股定理得出OC的长,再根据BC=OC﹣OB即可.
OCD是等腰直角三角形,再根据勾股定理得出OC的长,再根据BC=OC﹣OB即可.

(1)证明:连接DO,
∵AO=DO,
∴∠DAO=∠ADO=22.5°.
∴∠DOC=45°.
又∵∠ACD=2∠DAB,
∴∠ACD=∠DOC=45°.
∴∠ODC=90°.
又 OD是⊙O的半径,
∴CD是⊙O的切线.
(2)连接DB,
∵∠ACD=∠DOC=45°, ∴CD=OD
∵直径AB=2![]() ,
,
∴CD=OD=![]() ,OC=
,OC=![]() =2,
=2,
∴BC=OC﹣OB=2﹣![]() .
.

练习册系列答案
相关题目
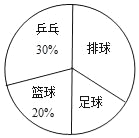
【题目】某校为了调查八年级学生参加“乒乓”、“篮球”、“足球”、“排球”四项体育活动的人数,学校从八年级随机抽取了部分学生进行调查,根据调查结果制作了如下不完整的统计表、统计图:
类别 | 频数(人数) | 频率 |
乒乓 | a | 0.3 |
篮球 | 20 | |
足球 | 15 | b |
排球 | ||
合计 | c | 1 |
请你根据以上信息解答下列各题:
(1)a= ;b= ;c= ;
(2)在扇形统计图中,排球所对应的圆心角是 度;
(3)若该校八年级共有600名学生,试估计该校八年级喜欢足球的人数?.