题目内容
已知∠AOB,
(1)如图1所示,点C在∠AOB的外部,OM平分∠AOC,ON平分∠BOC;
①若∠AOB=90°,∠BOC=30°,则∠MON=______°;
②若∠AOB=a,ABOC=β,求∠MON的度数;你能得到什么结论?
(2)如图2所示,点C在∠AOB的内部,OM平分∠AOC,ON平分∠BOC.上面②的结论还能成立吗?为什么?
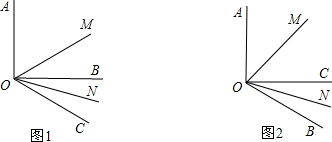
解:(1)①∵点C在∠AOB的外部,OM平分∠AOC,ON平分∠BOC,
∴∠MOC= (∠AOB+∠BOC)=60°,
(∠AOB+∠BOC)=60°,
又∵ON平分∠BOC,∠BOC=30°,
∴∠NOC=30°× =15°,
=15°,
∴∠MON=60°-45°=15°.
②∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= (α+β),∠CON=
(α+β),∠CON= β,
β,
∴∠MON=∠MOC-∠CON= (α+β)-
(α+β)- β=
β= α,
α,
∴∠MON= ∠AOB;
∠AOB;
(2)能成立,
理由:∵∠MOC= (α-β),∠CON=
(α-β),∠CON= β,
β,
∴∠MON=∠MOC-∠CON= (α-β)+
(α-β)+ β=
β= α,
α,
∴∠MON= ∠AOB.
∠AOB.
分析:(1)由OM平分∠AOC,ON平分∠BOC可知∠MON=∠MOB+∠NOB= (∠AOB+∠BOC),即可得到∠MON,(2)由∠MOC=
(∠AOB+∠BOC),即可得到∠MON,(2)由∠MOC= (α-β),∠CON=
(α-β),∠CON= β可得∠MON=∠MOC-∠CON,故能得到∠MON=
β可得∠MON=∠MOC-∠CON,故能得到∠MON= ∠AOB.
∠AOB.
点评:本题主要考查角的比较与运算,还涉及到角平分线等知识点.
∴∠MOC=
 (∠AOB+∠BOC)=60°,
(∠AOB+∠BOC)=60°,又∵ON平分∠BOC,∠BOC=30°,
∴∠NOC=30°×
 =15°,
=15°,∴∠MON=60°-45°=15°.
②∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=
 (α+β),∠CON=
(α+β),∠CON= β,
β,∴∠MON=∠MOC-∠CON=
 (α+β)-
(α+β)- β=
β= α,
α,∴∠MON=
 ∠AOB;
∠AOB;(2)能成立,
理由:∵∠MOC=
 (α-β),∠CON=
(α-β),∠CON= β,
β,∴∠MON=∠MOC-∠CON=
 (α-β)+
(α-β)+ β=
β= α,
α,∴∠MON=
 ∠AOB.
∠AOB.分析:(1)由OM平分∠AOC,ON平分∠BOC可知∠MON=∠MOB+∠NOB=
 (∠AOB+∠BOC),即可得到∠MON,(2)由∠MOC=
(∠AOB+∠BOC),即可得到∠MON,(2)由∠MOC= (α-β),∠CON=
(α-β),∠CON= β可得∠MON=∠MOC-∠CON,故能得到∠MON=
β可得∠MON=∠MOC-∠CON,故能得到∠MON= ∠AOB.
∠AOB.点评:本题主要考查角的比较与运算,还涉及到角平分线等知识点.

练习册系列答案
相关题目
 14、如图,已知∠AOB=30°,M为OB边上一点,以M为圆心、2cm为半径作M.若点⊙M在OB边上运动,则当OM=
14、如图,已知∠AOB=30°,M为OB边上一点,以M为圆心、2cm为半径作M.若点⊙M在OB边上运动,则当OM=
 如图,在平面直角坐标系中,已知△AOB,A(0,-3),B(-2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;
如图,在平面直角坐标系中,已知△AOB,A(0,-3),B(-2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;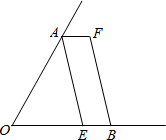 如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中
如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中