题目内容
如图1,在等腰梯形ABCD中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A、B在第一象限内。
(1) 求点E的坐标;
(2) 点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,
连结PN。设PE=x.△PMN的面积为S。
① 求S关于x的函数关系式;
② △PMN的面积是否存在最大值,若不存在,请说明理由。若存在,求出面积的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC)。现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2)。设运动时间为t秒,运动后的直角梯形为E′D′G′H′;探究:在运动过程中,等腰梯形ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式。


(1)E(1, )
)
(2)①当0≤X≤1时,S=
当1<X≤4时,S=-

②若0≤X≤1时,S=
若1<X≤4时,S=-

∵- <0 ∴S随X的增大而减小
<0 ∴S随X的增大而减小
∴S不存在最大值
∴综上所述,当0≤X≤1时,S存在最大值,最大值为
(3)当0≤t≤2时,直角梯形E′D′G′H′落在等腰梯形内部,这时重叠部分的面积即为直角梯形面积,y= ×(2+3)×
×(2+3)× =
=
当2<X≤4时,y= ×(4-t+5-t)×
×(4-t+5-t)× =-
=- t+
t+
当4<X≤5时,y=(5-t)× ×
× (5-t)=
(5-t)=  (5-t)²
(5-t)²
解析

 阅读快车系列答案
阅读快车系列答案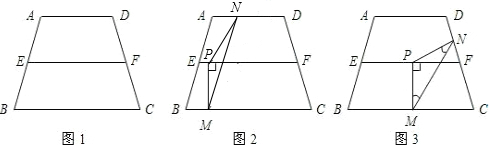
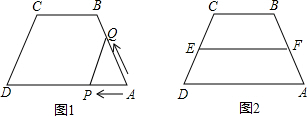 条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
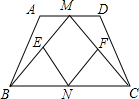 (2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:
(2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题: