��Ŀ����
����Ŀ�����ⱳ������![]() �У�
�У�![]() ���ϵĶ���
���ϵĶ���![]() ��
��![]() ��
��![]() �˶�����
�˶�����![]() ��
��![]() ���غϣ�����
���غϣ�����![]() ���
���![]() ͬʱ�������ɵ�
ͬʱ�������ɵ�![]() ��
��![]() ���ӳ��߷����˶���
���ӳ��߷����˶���![]() ����
����![]() �غϣ�������
�غϣ�������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���߶�
���߶�![]() ��һ��.
��һ��.
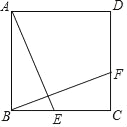
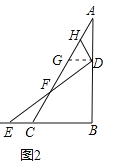
��1���������ԣ���ͼ����![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ���ҵ�
���ҵ�![]() ��
��![]() ���˶��ٶ���ȣ���֤��
���˶��ٶ���ȣ���֤��![]() .
.
С��ͬѧ���ֿ�������������˼·��������⣺
˼·һ������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����֤
����֤![]() ����֤
����֤![]() ���Ӷ�֤�ý��۳�����
���Ӷ�֤�ý��۳�����
˼·��������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����֤
����֤![]() ����֤
����֤![]() ���Ӷ�֤�ý��۳���.
���Ӷ�֤�ý��۳���.
������ѡһ��˼·����������д��С���֤�����̣��������ַ����������Ե�һ�ַ������֣�
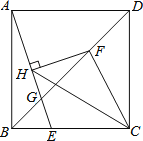
��2�����̽������ͼ������![]() �У�
��![]() ��
��![]() ���ҵ�
���ҵ�![]() ��
��![]() ���˶��ٶ�֮����
���˶��ٶ�֮����![]() ����
����![]() ��ֵ��
��ֵ��
��3��������չ����ͼ������![]() �У�
��![]() ��
��![]() ����
����![]() ���ҵ�
���ҵ�![]() ��
��![]() ���˶��ٶ���ȣ����ú�
���˶��ٶ���ȣ����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��ֱ��д�����������д�����̣�.
��ֱ��д�����������д�����̣�.
���𰸡���1��֤������������2��![]() ����3��
����3��![]() .
.
��������
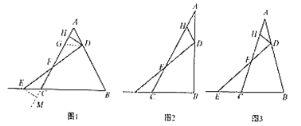
��1������D��DG��BC����AC�ڵ�G����֤����ADG�ǵȱ������Σ��ó�GD=AD=CE����֤��GH=AH����ASA֤����GDF�ա�CEF���ó�GF=CF�����ɵó����ۣ�
��2������D��DG��BC����AC�ڵ�G����֤��AH=GH=GD��AD=![]() GD��������AD=
GD��������AD=![]() CE���ó�GD=CE����֤����GDF�ա�CEF���ó�GF=CF�����ɵó����ۣ�
CE���ó�GD=CE����֤����GDF�ա�CEF���ó�GF=CF�����ɵó����ۣ�
��3������D��DG��BC����AC�ڵ�G����֤��DG=DH=AH����֤����ADG�ס�ABC����ADG�ס�DGH����DGH�ס�ABC���ó�![]() ����DGH�ס�ABC���ó�
����DGH�ס�ABC���ó�![]() ��֤����DFG�ס�EFC���ó�
��֤����DFG�ס�EFC���ó�![]() ��
��![]() �����ɵó������
�����ɵó������
�⣺��1��֤����ѡ��˼·һ��
����ͼ1������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ��
��![]() .
.
��![]() �ǵȱ�������.��
�ǵȱ�������.��![]() .
.
��![]() ����
����![]() .
.
��![]() ����
����![]() ��
��![]() .
.
��![]() .��
.��![]() .
.
��![]() ����
����![]() .
.
��2����ͼ2������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��![]() ��
��
��![]() ����
����![]() .
.
��![]() ��
��![]() .
.
�������֪��![]() ����
����![]() .
.
��![]() ����
����![]() ��
��![]() .
.
��![]() .��
.��![]() .
.
��![]() ����
����![]() .
.
��![]() .
.
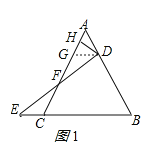
��3��![]() ���������£�
���������£�
����D��DG��BC����AC�ڵ�G����ͼ3��ʾ��
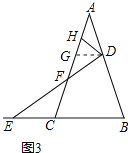
���ADG=��B����AGD=��ACB��
��AB=AC����BAC=36�㣬
���ACB=��B=��ADG=��AGD=72�㣬
�ߡ�ADH=��BAC=36�㣬
��AH=DH����DHG=72��=��AGD��
��DG=DH=AH����ADG�ס�ABC����ADG�ס�DGH��
![]() ��
��
���DGH�ס�ABC��
![]() ��
��
![]() ��
��
��DG��BC��
���DFG�ס�EFC��
![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
![]() .
.

 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�����Ŀ����ͼ��ABΪ��Oֱ������C�ǡ�O��һ���㣬����C����Oֱ��CD������B��BE��CD�ڵ�E����֪AB=6cm������AC�ij�Ϊx cm��B��E�����ľ���Ϊy cm(����C���A���B�غ�ʱ��y��ֵΪ0)��
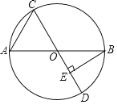
С������ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
(1)ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 0. 99 | 1. 89 | 2. 60 | 2. 98 | m | 0 |
������m��ֵΪ_____����������λС����
(2)����ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ
��

��3����ϻ����ĺ���ͼ������⣺��BE=2ʱ��AC�ij���ԼΪ cm.