题目内容
在△ABC中，∠A=50°，高BE，CF（或其延长线）交于点O，且点O不与B，C重合，则∠BOC=________．
130°或50°
分析：因为三角形的形状不明确，分∠BOC在三角形的内部和在三角形的外部两种情况，然后根据四边形的内角和定理和等角的余角相等的性质分别进行解答．
解答：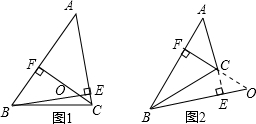
解：（1）如图1，当三角形为锐角三角形时，∠BOC在三角形内部，
∠BOC=360°-90°-90°-∠A=180°-50°=130°；
（2）如图2，当三角形为钝角三角形时，∠BOC在三角形外部，
∵BE⊥AC，CF⊥AB，
∴∠OEC=∠AFC=90°，
∵∠ACF=∠OCE，∠A=50°，
∴∠BOC=∠A=50°．
故应填130°或50°．
点评：本题主要运用四边形的内角和定理和直角三角形的性质求解，注意因为三角形的形状不明确，要分两种情况讨论．
分析：因为三角形的形状不明确，分∠BOC在三角形的内部和在三角形的外部两种情况，然后根据四边形的内角和定理和等角的余角相等的性质分别进行解答．
解答：
解：（1）如图1，当三角形为锐角三角形时，∠BOC在三角形内部，∠BOC=360°-90°-90°-∠A=180°-50°=130°；
（2）如图2，当三角形为钝角三角形时，∠BOC在三角形外部，
∵BE⊥AC，CF⊥AB，
∴∠OEC=∠AFC=90°，
∵∠ACF=∠OCE，∠A=50°，
∴∠BOC=∠A=50°．
故应填130°或50°．
点评：本题主要运用四边形的内角和定理和直角三角形的性质求解，注意因为三角形的形状不明确，要分两种情况讨论．
练习册系列答案
阅读快车系列答案
相关题目
23、如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
18、如图，在△ABC中，边AC的垂直平分线交BC于点D，交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm，则线段AE的长等于在△ABC中，∠C=90°，BC=12，AB=13，则tanA的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，a=
，b=
，c=2
，则最大边上的中线长为（ ）
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |