题目内容
如图,直线 与x轴、y轴分别交于B、A两点,且A、B两点的坐标分别为A(0,6)、B(8,0)。现将线段AB绕着点B按顺时针方向旋转90o,得到线段BC。
与x轴、y轴分别交于B、A两点,且A、B两点的坐标分别为A(0,6)、B(8,0)。现将线段AB绕着点B按顺时针方向旋转90o,得到线段BC。
(1)求直线 的函数解析式
的函数解析式
(2)求点C的坐标及△OBC的面积
(3)坐标轴上的是否存在一点P,使得△ABP的面积与△OBC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由。

 与x轴、y轴分别交于B、A两点,且A、B两点的坐标分别为A(0,6)、B(8,0)。现将线段AB绕着点B按顺时针方向旋转90o,得到线段BC。
与x轴、y轴分别交于B、A两点,且A、B两点的坐标分别为A(0,6)、B(8,0)。现将线段AB绕着点B按顺时针方向旋转90o,得到线段BC。(1)求直线
 的函数解析式
的函数解析式(2)求点C的坐标及△OBC的面积
(3)坐标轴上的是否存在一点P,使得△ABP的面积与△OBC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由。

(1) ;
;
(2)C点坐标为(14,8);32
(3)当P点在B点右边时,P点坐标为( ,0),当P点在B点左边时,P点坐标为(
,0),当P点在B点左边时,P点坐标为( ,0).
,0).
 ;
;(2)C点坐标为(14,8);32
(3)当P点在B点右边时,P点坐标为(
 ,0),当P点在B点左边时,P点坐标为(
,0),当P点在B点左边时,P点坐标为( ,0).
,0).试题分析:(1)先设直线方程为y=kx+b,然后把A、B两点坐标代入求出直线的解析式;
(2)利用线段AB绕着点B按顺时针方向旋转90o得到线段BC,得出BC的斜率及BC的长,然后根据两点距离公式求出C点的坐标,再根据三角形的面积公式求△OBC的面积;
(3)P点坐标分在x轴、y轴两种情况进行讨论.
点评:利用数形结合求解是解题的关键.

练习册系列答案
相关题目

 的值不小于-1。
的值不小于-1。 的图象经过的象限是( )
的图象经过的象限是( )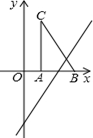

 千米/时,
千米/时, 千米/时。(2分)
千米/时。(2分) (
( 为常数)上有两点
为常数)上有两点 和
和 ,若
,若 ,则
,则 与
与 的大小关系是( )
的大小关系是( )

