题目内容
如果a-b>a+b,那么
- A.|a-b|>|a+b|
- B.ab<0
- C.-2b>2b
- D.-2a>2b
C
分析:A、D利用特例来说明问题(举出的特例必须符合已知条件),B、C利用等式性质来说明问题.
解答:A、∵a-b>a+b,
∴-b>b,
即b<0,
若a=-3,b=-4,
有a-b>a+b,
但是|a-b|<|a+b|,
故此选项错误;
B、由A知b<0,
若a<0,
那么有ab>0,
故此选项错误;
C、由A得
-b>b,
∴-2b>2b(不等式性质2),
故此选项正确;
D、若a=2,b=-1,
符合条件a-b>a+b,
但是-2a=-4,2b=-2,
∴-2a<2b,
故此选项错误.
故选C.
点评:不等式的性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
若字母的数值不确定,可利用特值来说明问题.
分析:A、D利用特例来说明问题(举出的特例必须符合已知条件),B、C利用等式性质来说明问题.
解答:A、∵a-b>a+b,
∴-b>b,
即b<0,
若a=-3,b=-4,
有a-b>a+b,
但是|a-b|<|a+b|,
故此选项错误;
B、由A知b<0,
若a<0,
那么有ab>0,
故此选项错误;
C、由A得
-b>b,
∴-2b>2b(不等式性质2),
故此选项正确;
D、若a=2,b=-1,
符合条件a-b>a+b,
但是-2a=-4,2b=-2,
∴-2a<2b,
故此选项错误.
故选C.
点评:不等式的性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
若字母的数值不确定,可利用特值来说明问题.

练习册系列答案
相关题目
如果关于x的不等式组
无解,则m的取值范围是( )
|
| A、m>3 | B、m≥3 |
| C、m<3 | D、m≤3 |
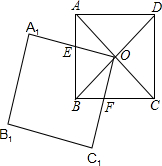 于点E,OC1交BC于点F.
于点E,OC1交BC于点F. ,请问小军至少几次进入迷宫中心?
,请问小军至少几次进入迷宫中心?