题目内容
.(8分)在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=35º,求∠ACF度数.
(1) 证明见解析.(2) ∠ACF=55º
【解析】
试题分析:(1)因为AB=CB,AE=CF.且∠ABC=90º根据斜边直角边定理可判定Rt△ABE≌Rt△CBF.
(2)由(1)知Rt△ABE≌Rt△CBF.所以∠EAB=∠FCB 所以∠ACF=∠FCB+∠ACB=∠EAB+∠ACB=90º-∠CAE=90º-35º=55º.
试题解析:(1)∵AB=CB,AE=CF.且∠ABC=90º ∴Rt△ABE≌Rt△CBF(HL)
(2)由(1)知Rt△ABE≌Rt△CBF.∴∠EAB=∠FCB ∴∠ACF=∠FCB+∠ACB=∠EAB+∠ACB=90º-∠CAE∵∠CAE=35º∴∠ACF=55º
考点:“HL”判定三角形全等,互余

练习册系列答案
相关题目
 B.
B.  C.
C.  D.
D. 




 B.
B.
 D.
D.

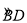 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.