Question

【题目】[新定义]: 为数轴上三点，若点到点的距离是点到点的距离的3倍，我们就称点的幸运点.

[特例感知]

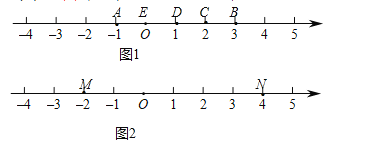
（1）如图1，点表示的数为-1，点表示的数为3.表示2的点到点的距离是3，到点的距离是1，那么点是的幸运点，

①的幸运点表示的数是________；

A.-1 B.0 C.1 D.2

②试说明的幸运点.

（2）如图2， 为数轴上两点，点所表示的数为-2，点所表示的数为4，

则的幸运点表示的数为________.

[拓展应用]

（3）如图3， 为数轴上两点，点所表示的数为-20，点所表示的数为40.有一只电子蚂蚁从点出发，以5个单位每秒的速度向左运动，到达点停止.当t为何值时，、和三个点中恰好有一个点为其余两点的幸运点?

Answer 1

【答案】（1） ①；②理由见解析；（2）7或2.5； （3）3秒、9秒、8秒或 4秒.

【解析】

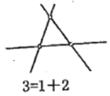
（1）①由题意可知，点0到B是到A点距离的3倍；②由数轴可知，AC=3，AE=1，可得AC=3AE；
（2）设[M，N]的幸运点为P，T表示的数为p，由题意可得|p+2|=3|p-4|，求解即可；
（3）由题意可得，BP=3t，AP=60-3t，分四种情况讨论：①当P是[A，B]的幸运点时，PA=3PB②当P是[B，A]的幸运点时，PB=3PA③当A是[B，P]的幸运点时，AB=3PA，④当B是[A，P]的幸运点时，AB=3PB．

解: （1） ①由题意可知，

∴，即点到点是到点距离的3倍，

点表示的数是0，故选.

②由数轴可知，，

∴，

∴的幸运点.

（2）设的幸运点为，设它表示的数为，

∴，

∴，

∴，

∴；

故答案为7或2.5；

（3）由题意可得， ，

①当的幸运点时，

∴，

∴；

②当的幸运点时，，

∴，

∴；

③当的幸运点时， ，

∴

∴；

④当的幸运点时，，

∴，

∴；

∴为3秒、9秒、8秒、 4秒时， 中恰好有一个点为其余两点的幸运点 .