题目内容
已知:梯形ABCD中,AD∥BC,AD=1,BD过梯形的高AE的中点F,且BD⊥DC,设AE=h,BC=a.(1)用含字母h的代数式表示a;
(2)若a、h是关于x的一元二次方程3x2-3(m+2)x+10m=0的两根,求sin∠DBC的值.
分析:(1)首先由Rt△AFD≌Rt△EFB,可得BF=FD,BE=1;且EF=
;且BD=BF;进而可用h表示出BD,BF的长,再根据Rt△BEF∽Rt△BDC,可得
=
;代入h的关系与BC=a可得答案;
(2)由根与系数的关系可得a+h=m+2,ah=
;结合(1)的结论,可得a,h的值,进而可得CD的长,再根据三角函数的定义,可得答案.
| h |
| 2 |
| BE |
| BF |
| BD |
| BC |
(2)由根与系数的关系可得a+h=m+2,ah=
| 10m |
| 3 |
解答: 解:(1)根据题意,AD∥BC,且AF=EF;
解:(1)根据题意,AD∥BC,且AF=EF;
易得Rt△AFD≌Rt△EFB,故BF=FD,BE=1;且EF=
;
由勾股定理可得:BF=
;又可得AD=2AF;
Rt△BEF与Rt△BDC中,有∠BEF=∠BDC=90°,∠B=∠B;
故Rt△BEF∽Rt△BDC,进而可得
=
;
化简可得:a=2(1+
);即a=2+
.
(2)若a、h是关于x的一元二次方程3x2-3(m+2)x+10m=0的两根,
则a+h=m+2,ah=
;
又有a=2+
;解可得a=20,h=6;
DC=
=16;
易得sin∠DBC=
=
.
 解:(1)根据题意,AD∥BC,且AF=EF;
解:(1)根据题意,AD∥BC,且AF=EF;易得Rt△AFD≌Rt△EFB,故BF=FD,BE=1;且EF=
| h |
| 2 |
由勾股定理可得:BF=
1+
|
Rt△BEF与Rt△BDC中,有∠BEF=∠BDC=90°,∠B=∠B;
故Rt△BEF∽Rt△BDC,进而可得
| BE |
| BF |
| BD |
| BC |
化简可得:a=2(1+
| h2 |
| 4 |
| h2 |
| 2 |
(2)若a、h是关于x的一元二次方程3x2-3(m+2)x+10m=0的两根,
则a+h=m+2,ah=
| 10m |
| 3 |
又有a=2+
| h2 |
| 2 |
DC=
| BC2-BD2 |
易得sin∠DBC=
| DC |
| BC |
| 4 |
| 5 |
点评:本题考查梯形,菱形、直角三角形的相关知识.解决此类题要懂得用梯形的常用辅助线,把梯形分割为菱形和直角三角形,从而由菱形和直角三角形的性质来求解.

练习册系列答案
相关题目
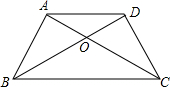 如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.
如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明. 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC= 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( ) 如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )
如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )