题目内容
 如图,已知⊙O中弦AB=2,弓形高CD=2-
如图,已知⊙O中弦AB=2,弓形高CD=2- ,求弓形ABC的面积.
,求弓形ABC的面积.
 解:连OA,OB,如图,
解:连OA,OB,如图,∵弓形高为CD,
∴CD过圆心O,
∴AD=BD=1,
设半径为R,CD=2-
 ,则OD=R-(2-
,则OD=R-(2- ),
),在Rt△AOD中,R2=[R-(2-
 )]2+12,解得R=2,
)]2+12,解得R=2,∴OD=
 ,
,∴∠AOD=30°,
∴∠AOB=60°,
所以S弓形ABC=S扇形OAB-S△OAB=
 -
- ×2×
×2× =
= -
- .
.分析:连OA,OB,由弓形高为CD,得到CD过圆心O,则AD=BD=1,设半径为R,在Rt△AOD中利用勾股定理得到R2=[R-(2-
 )]2+12,则R=2,得到∠AOB=60°,而S弓形ABC=S扇形OAB-S△OAB,然后根据扇形的面积公式与三角形的面积公式进行计算即可得到弓形ABC的面积.
)]2+12,则R=2,得到∠AOB=60°,而S弓形ABC=S扇形OAB-S△OAB,然后根据扇形的面积公式与三角形的面积公式进行计算即可得到弓形ABC的面积.点评:本题考查了扇形的面积公式:S=
 ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.也考查了弓形高的定义以及勾股定理.
lR,l为扇形的弧长,R为半径.也考查了弓形高的定义以及勾股定理. 
练习册系列答案
相关题目
 7、如图,已知⊙O中,半径OC垂直于弦AB,垂足为D,若OD=3,OA=5,则AB的长为( )
7、如图,已知⊙O中,半径OC垂直于弦AB,垂足为D,若OD=3,OA=5,则AB的长为( )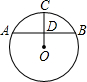 如图,已知⊙O中弦AB=2,弓形高CD=2-
如图,已知⊙O中弦AB=2,弓形高CD=2- (2012•宝安区二模)如图,已知⊙O中,半径OC⊥弦AB于点D,∠AOC=60°.
(2012•宝安区二模)如图,已知⊙O中,半径OC⊥弦AB于点D,∠AOC=60°. ,求弓形ABC的面积.
,求弓形ABC的面积.