题目内容
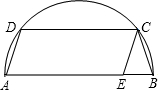 已知:如图,AB是半圆的直径,AB=10,梯形ABCD内接于半圆,CE∥AD交AB于E,BE=2,求∠A的余弦值.
已知:如图,AB是半圆的直径,AB=10,梯形ABCD内接于半圆,CE∥AD交AB于E,BE=2,求∠A的余弦值.
分析:根据平行线所夹的弧相等得到弧AD=弧BC,再根据在同圆中弧相等弦相等得到AD=BC,则四边形AECD为平行四边形,得到CD=AE=AB-BE=8.设圆心为O,作OG⊥CD于G,连OC,根据垂径定理得到DG=CG=4,利用勾股定理计算出OG,作DF⊥OA于F,则DF=OG=3,利用等腰梯形的性质计算出AF,再根据勾股定理求出AD,最后利用余弦的定义求解即可.
解答:解:连OD,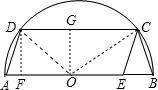 如图,
如图,
∵四边形ABCD为梯形,
∴CD∥AB,
∴∠AOD=∠ODC,∠BOC=∠OCD,
而∠ODC=∠OCD,
∴∠AOD=∠BOC,
∴弧AD=弧BC,
∴AD=BC
又∵CE∥AD,
∴四边形AECD为平行四边形,
∴CD=AE=AB-BE=8
设圆心为O,作OG⊥CD于G,连OC,
∴DG=CG=4.
∴OG=
=3.
作DF⊥OA于F,则DF=OG=3,
AF=OA-OF=OA-DG=1.
∴AD=
=
.
∴∠A的余弦:cosA=
=
.
 如图,
如图,∵四边形ABCD为梯形,
∴CD∥AB,
∴∠AOD=∠ODC,∠BOC=∠OCD,
而∠ODC=∠OCD,
∴∠AOD=∠BOC,
∴弧AD=弧BC,
∴AD=BC
又∵CE∥AD,
∴四边形AECD为平行四边形,
∴CD=AE=AB-BE=8
设圆心为O,作OG⊥CD于G,连OC,
∴DG=CG=4.
∴OG=
| OC2-CG2 |
作DF⊥OA于F,则DF=OG=3,
AF=OA-OF=OA-DG=1.
∴AD=
| AF2+DF2 |
| 10 |
∴∠A的余弦:cosA=
| 1 | ||
|
| ||
| 10 |
点评:本题考查了圆心角、弧、弦的关系;也考查了垂径定理和勾股定理以及等腰梯形的性质.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
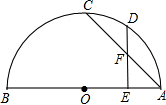 已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
 =-
=- ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.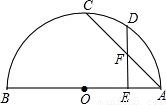
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.