题目内容
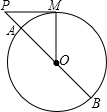如图，过⊙O的直径BA的延长线上一点P，作⊙O的切线PM，M为切点，如果PM=OM，则PA：PB=________．
（3-2
）：1
分析：可连接AM、BM，根据切线性质可知∠PMA=∠PBM，所以可知△PAM∽△PMB，PA•PB=PM2，再根据边即可确定PA：PB的值．
解答：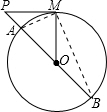
解：根据题意，连接AM、BM，
由切线性质知，∠PMA=∠PBM，∠P为公共角，
∴△PAM∽△PMB，
∴由对应边成比例知PAPB=PM2，
设边长为r，即PM=OM=r，
∴AB=2r，PB=PA+2r，
∴PA（PA+2r）=r2，
解得PA=（-1）r（舍负），
∴PB=（+1）r，
∴PA：PB=（3-2）：1．
点评：本题考查了切线性质，是基础题型．
）：1分析：可连接AM、BM，根据切线性质可知∠PMA=∠PBM，所以可知△PAM∽△PMB，PA•PB=PM2，再根据边即可确定PA：PB的值．
解答：
解：根据题意，连接AM、BM，由切线性质知，∠PMA=∠PBM，∠P为公共角，
∴△PAM∽△PMB，
∴由对应边成比例知PAPB=PM2，
设边长为r，即PM=OM=r，
∴AB=2r，PB=PA+2r，
∴PA（PA+2r）=r2，
解得PA=（
-1）r（舍负），∴PB=（
+1）r，∴PA：PB=（3-2
）：1．点评：本题考查了切线性质，是基础题型．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13、如图，过⊙O的直径AB上两点M，N，分别作弦CD，EF，若CD∥EF，AC=BF．
如图，过⊙O的直径BA的延长线上一点P，作⊙O的切线PM，M为切点，如果PM=OM，则PA：PB=
