题目内容
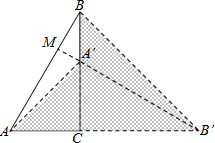 将直角△ABC绕直角顶点C旋转,使点A落在BC边上的点A′,请你先证明A′B′⊥AB,并利用阴影部分面积完成勾股定理的证明.
将直角△ABC绕直角顶点C旋转,使点A落在BC边上的点A′,请你先证明A′B′⊥AB,并利用阴影部分面积完成勾股定理的证明.
已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.
求证:a2+b2=c2.
证明:作△A′B′C≌△ABC,使点A的对应点A′在边BC上,
连接AA′、BB′,延长B′A′交AB于点M.
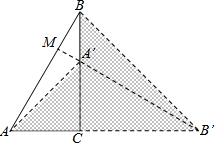 证明:作△A′B′C≌△ABC,使点A的对应点A′在边BC上,
证明:作△A′B′C≌△ABC,使点A的对应点A′在边BC上,连接AA′、BB′,延长B′A′交AB于点M,
∵∠A′B′C=∠ABC,∠BA′M=∠B′A′C,
∴∠BMA′=∠BCA=90°,
∴A′B′⊥AB,
∵△A′B′C≌△ABC,
∴AC=A′C=b,BC=B′C=a,AB=A′B′=c,
∵S△ACA′+S△BCB′=S△ABB′-S△AA′B,
∴
 b2+
b2+ a2=
a2= c(c+A′M)-
c(c+A′M)- cA′M,
cA′M,∴
 b2+
b2+ a2=
a2= c2,
c2,∴a2+b2=c2.
分析:首先作△A′B′C≌△ABC,再利用S△ACA′+S△BCB′=S△ABB′-S△AA′B,进而得出a2+b2=c2.
点评:此题主要考查了勾股定理的证明,根据全等三角形的性质以及三角形面积求法得出S△ACA′+S△BCB′=S△ABB′-S△AA′B是解决问题的关键.

练习册系列答案
相关题目
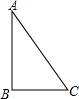 如图,将Rt△ABC绕直角边AB旋转一周,所得的几何体的主视图是( )
如图,将Rt△ABC绕直角边AB旋转一周,所得的几何体的主视图是( )A、 | B、 | C、 | D、 |

 如图所示,将直角△ABC绕点C逆时针旋转90°至A1B1C1的位置,已知AB=10,BC=6,M是A1B1的中点,则AM=
如图所示,将直角△ABC绕点C逆时针旋转90°至A1B1C1的位置,已知AB=10,BC=6,M是A1B1的中点,则AM= 如图所示,将直角△ABC绕点C逆时针旋转90°至A1B1C的位置,已知AB=10,BC=6,M是A1B1的中点,则AM的值为( )
如图所示,将直角△ABC绕点C逆时针旋转90°至A1B1C的位置,已知AB=10,BC=6,M是A1B1的中点,则AM的值为( )