题目内容
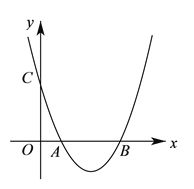
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 左
左![]() 右),与
右),与![]() 轴交于
轴交于![]() 点
点![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )若
)若![]() 为二次函数
为二次函数![]() 图象的顶点,求证:
图象的顶点,求证: ![]() .
.
(![]() )若
)若![]() 为二次函数
为二次函数![]() 图象上一点,且
图象上一点,且![]() ,求
,求![]() 点的坐标.
点的坐标.
【答案】(1)1;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)把![]() 点
点![]() 代入
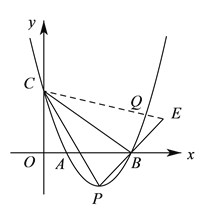
代入![]() 即可求得a值;(2)先求得抛物线的顶点坐标,利用勾股定理求得AC、BC、PC、PB的值,再利用三边对应成比例的两个三角形相似判定
即可求得a值;(2)先求得抛物线的顶点坐标,利用勾股定理求得AC、BC、PC、PB的值,再利用三边对应成比例的两个三角形相似判定![]() ,即可得结论;(3)分两种情况:当Q在BC的下方时,由(2)可知,点Q和点P重合;当点Q在BC的上方时,连接
,即可得结论;(3)分两种情况:当Q在BC的下方时,由(2)可知,点Q和点P重合;当点Q在BC的上方时,连接![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() 交二次函数图象于点
交二次函数图象于点![]() .先求得点E的坐标,再求得EC的解析式,直线EC与抛物线的交点坐标即为点Q的坐标.
.先求得点E的坐标,再求得EC的解析式,直线EC与抛物线的交点坐标即为点Q的坐标.
试题解析:
(![]() )∵
)∵![]() 与
与![]() 轴交于点
轴交于点![]() .
.
∴![]() ,
,
∴![]() .
.
(![]() )连接
)连接![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]() .
.
![]() .
.
![]() .
.
∵![]() ,
, ![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
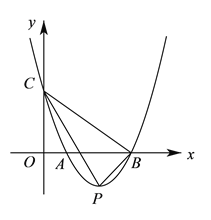
(![]() )连接
)连接![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() .
.
∵![]() ,
, ![]() .
.
∴![]() ,
,
∴![]() ,
, ![]() .
.
∴![]() 和
和![]() 的中点为
的中点为![]() .
.
∴![]() .
.
连接![]() 交二次函数图象于点
交二次函数图象于点![]() .
.
由(![]() )可知,当
)可知,当![]() 在顶点
在顶点![]() 时,
时, ![]() ,
,
∵![]() .
.
∴![]() .
.
∴![]() 是
是![]() 的垂直平分线.
的垂直平分线.
∴![]() .
.
∴![]() .
.
设![]() 所在直线:
所在直线: ![]() ,
,
∴将![]() 代入得
代入得![]() ,
, ![]() .
.
∴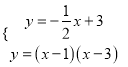 .
.
解得![]() 或
或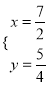 .
.
∴![]() 或
或![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目