题目内容
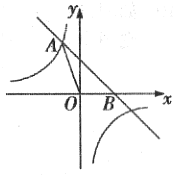
【题目】如图，直线y=﹣x+2与反比例函数y=
的图象相交于点A(a，3)，且与x轴相交于点B．
（1）求该反比例函数的表达式；
（2）写出直线y=﹣x+2向下平移2个单位的直线解析式，并求出这条直线与双曲线的交点坐标
【答案】（1）y=﹣
；（2）y=﹣x，(
，)或(﹣，﹣)
【解析】
（1）把A的坐标代入直线的解析式就可求得
，然后把（-1，3）代入
可求得k，从而求得反比例函数的解析式；
（2）利用直线平移时k的值不变，只有b发生变化即可写出向下平移2个单位后的解析式，再解方程组
，即可求得直线与双曲线的交点坐标．
(1)∵点A(，3)在直线
上．
∴
，
∴
，
∴A(
，3)
∵点A(，3)在反比例函数y=
的图象上，
∴3=
，
∴k=
，
∴该反比例函数的表达式为：y=
；
(2) 直线
向下平移2个单位后的解析式为
，
解方程组，
得：
或
，
∴交点坐标为(
，)、(
，) ．
练习册系列答案
相关题目
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销
件．已知产销两种产品的有关信息如下表：
产品 | 每件售价（万元） | 每件成本（万元） | 每年其他费用（万元） | 每年最大产销量（件） |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中
为常数，且
．
（1）若产销甲、乙两种产品的年利润分别为
万元、
万元，直接写出、与的函数关系式（写出自变量的取值范围）；
（2）分别求出产销两种产品的最大年利润；
（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．
