题目内容

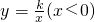如图，点P（-2，3），过P作PC∥x轴，PB∥y轴，并分别交双曲 $数学公式$ 于C、B两点，连接OB、OC，若S_{四边形OBPC}=4，则k=________．

-2
分析：先求出点B、C的坐标，延长PB交x轴于点E，延长PC交y轴于点F，利用S_{四边形OBPC}=S_矩形PEOF-S_△OBE-S_△OCF，列式计算即可求出k值．
解答：

解：∵点P（-2，3），过P作PC∥x轴，PB∥y轴，
∴当x=-2时，y=- $\text{[math]}$ ，当y=3时，x= $\text{[math]}$ ，
∴点B、C的坐标为B（-2， $\text{[math]}$ ），C（ $\text{[math]}$ ，3），
延长PB交x轴于点E，延长PC交y轴于点F，
则S_{四边形OBPC}=S_矩形PEOF-S_△OBE-S_△OCF，
=|-2|×3- $\text{[math]}$ ×|-2|•| $\text{[math]}$ |- $\text{[math]}$ ×| $\text{[math]}$ |×3，
=6-|k|，
根据图象可得k＜0，
又∵S_{四边形OBPC}=4，
∴6+k=4，
解得k=-2．
故答案为：-2．
点评：本题主要考查了反比例函数图象的性质，根据反比例函数解析式表示出点B、C的坐标，利用“割补法”把不规则四边形的面积利用规则的矩形与三角形的面积表示出来是解题的关键，难度中等．