题目内容
 如图,直线y=-mx-2与双曲线
如图,直线y=-mx-2与双曲线 交于点A,与x轴,y轴分别交于点B,C;AD⊥x轴于点D,tan∠DAB=
交于点A,与x轴,y轴分别交于点B,C;AD⊥x轴于点D,tan∠DAB= ;如果S△ADB=
;如果S△ADB= S△COB,那么k=________.
S△COB,那么k=________.
- -1
-1
分析:要求k的值,由于点A在双曲线 上,所以只需求出点A的坐标即可.首先把B(-1,0)代入y=-mx-2,可求出m的值,得到一次函数的解析式,再通过证明△ADB∽△COB,根据相似三角形的性质求出OD的长,根据三角函数的知识求出AD的长,从而得到A点坐标,代入双曲线
上,所以只需求出点A的坐标即可.首先把B(-1,0)代入y=-mx-2,可求出m的值,得到一次函数的解析式,再通过证明△ADB∽△COB,根据相似三角形的性质求出OD的长,根据三角函数的知识求出AD的长,从而得到A点坐标,代入双曲线 ,得到k的值.
,得到k的值.
解答:把B(-1,0)代入y=-mx-2,
得m-2=0,解得m=2.
∴y=-2x-2.
在△ADB与△COB中,∠ADB=∠COB=90°,∠ABD=∠CBO,
∴△ADB∽△COB,
∴S△ADB:S△COB=(DB:OB)2=1:2,
∴DB= ,
,
∴OD=OB+BD=1+ .
.
在△ADB中,∠ADB=90°,tan∠DAB=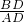 =
= ,
,
∴AD=2BD= .
.
∴A点坐标为(-1- ,
, ),
),
∴k=(-1- )•
)• =-
=- -1.
-1.
点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数 中k的几何意义.同时考查了相似三角形的性质及三角函数的知识,有一定的难度.
中k的几何意义.同时考查了相似三角形的性质及三角函数的知识,有一定的难度.
 -1
-1分析:要求k的值,由于点A在双曲线
 上,所以只需求出点A的坐标即可.首先把B(-1,0)代入y=-mx-2,可求出m的值,得到一次函数的解析式,再通过证明△ADB∽△COB,根据相似三角形的性质求出OD的长,根据三角函数的知识求出AD的长,从而得到A点坐标,代入双曲线
上,所以只需求出点A的坐标即可.首先把B(-1,0)代入y=-mx-2,可求出m的值,得到一次函数的解析式,再通过证明△ADB∽△COB,根据相似三角形的性质求出OD的长,根据三角函数的知识求出AD的长,从而得到A点坐标,代入双曲线 ,得到k的值.
,得到k的值.解答:把B(-1,0)代入y=-mx-2,
得m-2=0,解得m=2.
∴y=-2x-2.
在△ADB与△COB中,∠ADB=∠COB=90°,∠ABD=∠CBO,
∴△ADB∽△COB,
∴S△ADB:S△COB=(DB:OB)2=1:2,
∴DB=
 ,
,∴OD=OB+BD=1+
 .
.在△ADB中,∠ADB=90°,tan∠DAB=
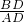 =
= ,
,∴AD=2BD=
 .
.∴A点坐标为(-1-
 ,
, ),
),∴k=(-1-
 )•
)• =-
=- -1.
-1.点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数
 中k的几何意义.同时考查了相似三角形的性质及三角函数的知识,有一定的难度.
中k的几何意义.同时考查了相似三角形的性质及三角函数的知识,有一定的难度. 
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y= 如图,直线y1=mx+4与x轴、y轴分别交于A点、B点,且与反比例函数y2=
如图,直线y1=mx+4与x轴、y轴分别交于A点、B点,且与反比例函数y2= 如图,直线y=mx与双曲线
如图,直线y=mx与双曲线 如图,直线y=mx+n与双曲线y=
如图,直线y=mx+n与双曲线y= 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=