题目内容
【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
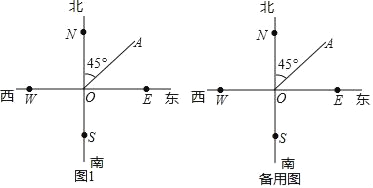
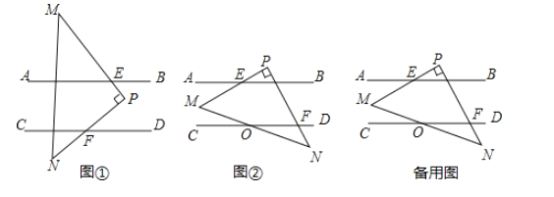
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

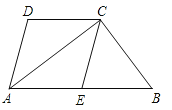
(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
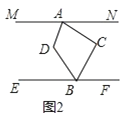
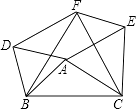
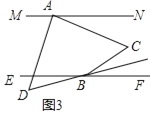
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)∠ADB=50°;(2)∠ADB=180°-![]() ∠ACB,证明见解析;(3)∠ADB=90°-
∠ACB,证明见解析;(3)∠ADB=90°-![]() ∠ACB.
∠ACB.
【解析】
(1)如图1,根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG,根据角平分线的定义得到![]() ,即可得到结论;
,即可得到结论;
(2)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据角平分线的定义得到![]() ,根据平角的定义即可得到结论;
,根据平角的定义即可得到结论;
(3)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据平行线的定义得到![]() ,根据四边形的内角和和角的和差即可得到结论.
,根据四边形的内角和和角的和差即可得到结论.
(1)如图1,过C作CG∥MN,DH∥MN,
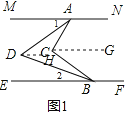
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠MAC=∠ACG,∠EBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴![]() ,
,
∴![]() ;
;
∵∠ACB=100°,
∴∠ADB=50°;
(2)如图2,过C作CG∥MN,DH∥MN,
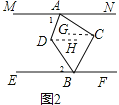
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴![]()
∴![]()
![]()
![]() ,
,
∴![]() ;
;
(3)如图3,过C作CG∥MN,DH∥MN,
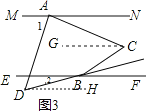
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠FBC的平分线相交于点D,
∴![]()
∵![]()
![]()
![]()
![]() .
.
∴![]()

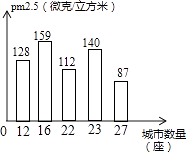
【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?
![]() 本星期内每股最低价多少元?
本星期内每股最低价多少元?
![]() 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少?