题目内容
如图，在△ABC中，∠C=20°，CA=CB，则△ABC的外角∠ABD=考点：等腰三角形的性质
专题：
分析：由CA=CB，可得∠A=∠ABC，且由∠C=20°，可求得∠ABC，则可求得∠ABD．
解答：解：∵CA=CB，∠C=20°，
∴∠A=∠ABC=
=80°，
∴∠ABD=180°-∠ABC=180°-80°=100°，
故答案为：100．
∴∠A=∠ABC=
| 180°-20° |
| 2 |
∴∠ABD=180°-∠ABC=180°-80°=100°，
故答案为：100．
点评：本题主要考查等腰三角形的性质，掌握等边对等角是解题的关键，注意三角形内角和定理的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列各数中，负数是（ ）
| A、-（-6） |
| B、-|-6| |
| C、（-6）2 |
| D、-（-6）3 |
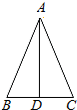如图，△ABC中，AB=AC，D为BC的中点，以下结论：（1）△ABD≌△ACD；
（2）AD⊥BC；
（3）∠B=∠C；
（4）AD是△ABC的角平分线．
其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，在△ABC中，AB=AC=BD，且D为BC上一点，CD=AD，则∠B的度数为（ ）| A、30° | B、36° |
| C、40° | D、45° |
以下列每组长度的三条线段为边能组成三角形的是（ ）
| A、2、3、6 |
| B、2、4、6 |
| C、2、2、4 |
| D、6、6、6 |
若分式
的值为0，则x的取值是（ ）
| |x|-1 |
| x-1 |
| A、x=1 | B、x=-1 |
| C、x=±1 | D、x=0 |