题目内容
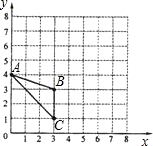 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.
(1)图中点A的坐标为______;点C的坐标为______;
(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)求(2)中线段CA旋转到C′A′所扫过的面积.
解:(1)A(0,4),C(3,1);
(2)如图,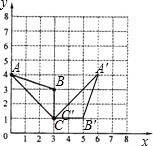
(3)∵AC=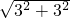 =3
=3 ,∠ACA′=90°,
,∠ACA′=90°,
∴S扇形CAA′= =
= .
.
分析:(1)在直角坐标系中读出A的坐标,点C的坐标;
(2)根据旋转的旋转画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)(2)中线段CA旋转到C′A′所扫过的图形为扇形,且圆心角为90度,半径CA利用勾股定理求得,然后利用扇形的面积公式:S= 计算即可.
计算即可.
点评:本题考查了扇形的面积公式:S= ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.
lR,l为扇形的弧长,R为半径.
(2)如图,

(3)∵AC=
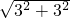 =3
=3 ,∠ACA′=90°,
,∠ACA′=90°,∴S扇形CAA′=
 =
= .
.分析:(1)在直角坐标系中读出A的坐标,点C的坐标;
(2)根据旋转的旋转画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)(2)中线段CA旋转到C′A′所扫过的图形为扇形,且圆心角为90度,半径CA利用勾股定理求得,然后利用扇形的面积公式:S=
 计算即可.
计算即可.点评:本题考查了扇形的面积公式:S=
 ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.
lR,l为扇形的弧长,R为半径. 
练习册系列答案
相关题目
 7、已知△ABC在平面直角坐标系的位置如图所示,将△ABC向右平移6个单位,则平移后A点的坐标是( )
7、已知△ABC在平面直角坐标系的位置如图所示,将△ABC向右平移6个单位,则平移后A点的坐标是( ) 18、已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).
18、已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度). 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.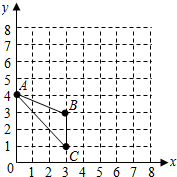 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示. ABC平移到△A1B1C1,使点A变换为点A1,点B1、C1分别是点B、C的对应点.
ABC平移到△A1B1C1,使点A变换为点A1,点B1、C1分别是点B、C的对应点.